Schultz, D. M., P. N. Schumacher, and C. A. Doswell III, 2000: The intricacies of instabilities. Mon. Wea. Rev., 128, 4143-4148. [AMS] [PDF] [HTML]

© Copyright 2000, American Meteorological Society

The Intricacies of Instabilities

David M. Schultz
NOAA/National Severe Storms Laboratory, Norman, Oklahoma

Philip N. Schumacher
NOAA/National Weather Service, Sioux Falls, South Dakota

Charles A. Doswell III
NOAA/National Severe Storms Laboratory, Norman, Oklahoma

NOTES AND CORRESPONDENCE
Monthly Weather Review
Received April 19, 2000; Revised May 30, 2000
Published in the December 2000 issue: pp. 4143-4148

To be published with and after
Sherwood, S. C., 2000: On moist instability. Mon. Wea. Rev., 128, 4139-4142.

Corresponding author address:
Dr. David M. Schultz
NOAA/National Severe Storms Laboratory
1313 Halley Circle
Norman, OK 73069
E-mail: schultz@nssl.noaa.gov

In response to Sherwood's comments and in an attempt to restore proper usage of terminology associated with moist instability, the early history of moist instability is reviewed. This review shows that many of Sherwood's concerns about the terminology were understood at the time of their origination. Definitions of conditional instability include both the lapse-rate definition (i.e., the environmental lapse rate lies between the dry- and the moist-adiabatic lapse rates) and the available-energy definition (i.e., a parcel possesses positive buoyant energy; also called latent instability), neither of which can be considered an instability in the classic sense. Furthermore, the lapse-rate definition is really a statement of uncertainty about instability. The uncertainty can be resolved by including the effects of moisture through a consideration of the available-energy definition (i.e., convective available potential energy, CAPE) or potential instability. It is shown that such misunderstandings about conditional instability were likely due to the simplifications resulting from the substitution of lapse rates for buoyancy in the vertical acceleration equation. Despite these valid concerns about the value of the lapse-rate definition of conditional instability, consideration of the lapse rate and moisture separately can be useful in some contexts (e.g., the ingredients-based methodology for forecasting deep, moist convection). It is argued that the release of potential (or convective) instability through layer lifting may occur in association with fronts, rather than with isolated convection, the terminology ``convective'' being an unfortunate modifier. The merits and demerits of slantwise convective available potential energy (SCAPE) are discussed, with the hope of improving diagnostic methodologies for assessing slantwise convection. Finally, it is argued that, when assessing precipitation events, undue emphasis may appear to be placed on instability, rather than the forcing for ascent, which should be of primary importance.

1  Introduction

Sherwood (2000) raises some excellent points regarding usage of the term conditional instability in atmospheric science. He discusses two ways that conditional instability is commonly used: the lapse-rate definition (i.e., the environmental lapse rate lies between the dry- and the moist-adiabatic lapse rates) and the available-energy definition (i.e., a parcel possesses positive buoyant energy). As Sherwood argues, the lapse-rate definition does not fit the strict definition of an instability and the available-energy definition is a subcritical instability, arguments with which we agree fully. Despite his valid concerns, we argue that the lapse-rate definition is useful in some contexts.

Sherwood's comments lead to questions about how the terminology for moist instability arose. Why would the founding fathers of scientific meteorology use the terms conditional and potential (convective) instability for situations that are not even instabilities in the strictest sense? As will be demonstrated in this paper, they appear to have understood the subtleties of this terminology-more recently, some meteorologists appear to have forgotten them.

Sherwood's concerns also affect the analogy Schultz and Schumacher (1999) drew between moist gravitational instability and moist symmetric instability through the ingredients-based methodology for forecasting deep moist gravitational convection (e.g., McNulty 1978, 1995; Doswell 1987; Johns and Doswell 1992). Consequently, in our response, we wish to differentiate among our concerns about the application of the terminology associated with conditional instability (section 2), potential instability (section 3), the ingredients-based methodology (section 4), and moist symmetric instability (section 5). Concluding thoughts are found in section 6.

2  Conditional instability

In section 2a, the origins of the terminology for conditional instability are explored. The fallacies noted by Sherwood were actually understood at the time this terminology was defined in the 1930's, but a popular mathematical derivation demonstrating the supposed equivalence between the lapse-rate and the available-energy definitions of conditional instability (reproduced in section 2b) appears to have reinforced these fallacies, or at least caused them to be more readily forgotten.

2a  Historical perspective

The mathematical basis for the vertical stability of moist atmospheres appears to have its roots in the 1860's (e.g., Kutzbach 1979, 53-58). Independently, Reye (1864) in Germany and Peslin (1868) in France determined the lapse-rate criteria for what is now commonly termed absolute instability (environmental lapse rate greater than the dry-adiabatic lapse rate), absolute stability (environmental lapse rate less than the moist-adiabatic lapse rate), and conditional instability. At one time, conditional instability was known as ``liability of environment for saturated air" (Shaw 1926) or ``Feucht-labilität" (Refsdal 1930) before Rossby (1932) apparently coined the term now used today for environmental lapse rates between the dry- and moist-adiabatic lapse rates.

Conditional instability was explored further by Normand (1938), who recognized two of the problems identified by Sherwood. First, Normand (1938) acknowledged that an unsaturated conditionally unstable atmosphere is not a true instability in the sense that a linearized stability analysis would show infinitesimal perturbations growing at an exponential rate. In fact, for unsaturated conditionally unstable environments, finite displacements of unsaturated air parcels are needed in order to realize the instability (if it can be realized at all). Normand (1938, p. 52) described this state as ``instability for big upward displacements" or latent instability (Normand 1931a,b), analogous to the metastability or subcritical-instability concepts from fluid dynamics (e.g., Sohoni and Paranjpe 1937; Emanuel 1997; Sherwood 2000). The term latent instability, however, appears to have fallen into disuse since Normand's time.

Second, as Sherwood has illustrated in his Fig. 1, a state of conditional instability is really a statement of uncertainty with regard to stability. Normand (1938) understood that not all conditionally unstable atmospheres lead to unsettled weather. Because moisture is not accounted for in assessing conditional instability (i.e., q_es or q_e^*, the saturated equivalent potential temperature, is a function of temperature and pressure only, not of humidity), some measure of the moisture profile is needed to refine the classification of stability. Thus, the concept of available energy was introduced. Normand (1938) subdivided conditional instability into additional classifications based on what we now term convective inhibition (CIN) and convective available potential energy (CAPE).¹

Table 1 illustrates Normand's classification scheme. When a conditionally unstable atmosphere is saturated, then a true state of instability is present since any perturbation will grow. [For example, Kain and Fritsch (1998) and Bryan and Fritsch (2000) demonstrate that layers of saturated conditional instability exist in advance of squall lines, features they call moist-adiabatic unstable layers.] When a conditionally unstable atmosphere is unsaturated, CAPE must be evaluated to determine the degree of instability. If the conditionally unstable layer is surmounted by a stable layer such that CAPE is zero, for example, then Normand (1938) used the oxymoron stable conditional instability; that is, no vertical displacement of parcels, however large, will produce any positive buoyancy. A conditionally unstable atmosphere with positive CAPE is viewed as possessing a subcritical or latent instability. If CAPE exceeds CIN, then this state is termed termed real (latent) instability (Sohoni and Paranjpe 1937). If CIN exceeds CAPE, implying that more energy is put into lifting parcels than is obtained once convection starts, then Sohoni and Paranjpe (1937) term this situation pseudoinstability or pseudolatent instability. Whereas Sohoni and Paranjpe (1937) and Normand (1938) compared the relative sizes of CIN and CAPE to determine stability, modern forecasters consider each separately. CIN is an important element in the forecast process, but, in our opinion, not in classifying stability [see also Petterssen (1956, 139-140)]. Thus, as Sherwood has argued, the available-energy definition for assessing instability appears to be much more useful than the lapse-rate definition, a point we will return to in section 4. For the purposes of this paper, ``conditional instability'' will hereafter refer to the lapse-rate definition.

2b  Mathematical basis

The previous section showed that not all soundings possessing layers with conditionally unstable lapse rates can produce parcel instability. The traditional association between conditional instability and parcel instability, however, may owe its origins to the following simple, but flawed, analysis using parcel theory. Parcel theory employs observed or model-forecast soundings to assess instability. In forecasting, these so-called environmental soundings approximate the conditions that exist prior to convective initiation, presumably because they are meant to represent the ``environment" that storms will form in. There are caveats with this interpretation, however. First, defining a sounding representative enough to be considered ``environmental" has a host of problems (e.g., Brooks et al. 1994). Second, as mentioned in Schultz and Schumacher (1999, section 3e), parcel theory neglects potentially important processes (e.g., mixing, ice phase). Finally, processes that lift parcels in the atmosphere also affect the ``environment" such that the sounding evolves during parcel ascent (e.g., Normand 1938). Therefore, although the parcel method is not without its problems, we are faced with using it to assess instability, until a new paradigm for moist convection is developed.

Following Hess (1959, 97-98), the vertical acceleration of a parcel ([(d²z)/( dt²)]) is proportional to the acceleration due to gravity (g) times the difference between the parcel temperature (T_p) and the environmental temperature (T_e):

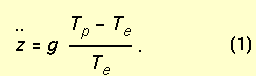
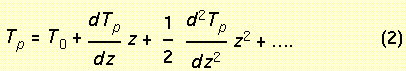
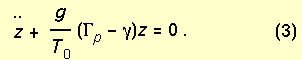
Equation (3) will be a linear ordinary differential equation when the coefficient of z, g(G_p - g)/T₀, is constant with height. In that case, if G_p - g < 0, perturbations will grow exponentially in time, resulting in release of the instability. Thus, instability in the classic sense will be manifest given two conditions: (a) G_p is constant over the displacement z (i.e., the parcel remains saturated or unsaturated) and (b) g is constant over the displacement z. Clearly, for conditional instability, (a) would only be met if the parcel was initially saturated. Thus, accounting for the process by which finite displacements of unsaturated air parcels become saturated is unaddressed by this formulation. In general, (b) is not met either, as the lapse rate of the environmental sounding typically varies with height.³ Thus, the problems with this derivation are that the theory does not include the finite displacement necessary to reach saturation and that the linearization is often not valid, except in a very small neighborhood about the original state. Thus, the standard mathematical exercise for equating parcel/environment temperatures with parcel/environment lapse rates is not appropriate for conditional instability in general.

This point is significant because situations occur in the atmosphere where parcel stability differs from lapse-rate stability. Consider a sounding with sufficient low-level moisture and warmth to yield substantial CAPE for some low-level parcel, from its level of free convection (LFC) to its equilibrium level (e.g., at 250 hPa). As that parcel ascends along its associated moist adiabat, it is quite possible that in some layer (e.g., 400-450 hPa), the environmental lapse rate could be absolutely stable, even to the extent of having a negative lapse rate. The presence of absolute stability in that layer, however, does not alter the fact that the ascending parcel is positively buoyant. In such cases, the stability of the layer (as defined by its lapse rate) can differ dramatically from the parcel stability (as defined by its buoyancy). Hence, it may be preferable in the future to use the term conditional instability only for the lapse-rate definition and resurrect the term latent instability for the energy-based definition.

3  Potential instability

As discussed in the previous section, the inability of the lapse-rate definition of conditional instability to ascertain unambiguously parcel stability led to the realization that the vertical profile of moisture needs to be accounted for. Thus, potential (or convective) instability was developed. The historical basis is described in section 3a. Although the layer-lifting mechanism originally perceived to release potential instability is generally not believed to occur in isolated convective storms, certain situations, discussed in section 3b, may be found where layer lifting of parcels produces deep moist convection.

3a  Historical perspective

The concept of convective instability was originally defined by Rossby (1932) to be when one of the three following equivalent conditions is met over a layer of the atmosphere: (1) the lapse rate of wet-bulb temperature exceeds the moist-adiabatic lapse rate, (2) the equivalent potential temperature q_e decreases with height, or (3) the wet-bulb potential temperature q_w decreases with height. As formulated by Rossby, convective instability is present when a layer bounded by two pressure levels is lifted such that the bottom of that layer reaches saturation before the top does. Continued ascent steepens the lapse rate within the layer by the difference between the dry- and moist-adiabatic lapse rates, until the entire layer reaches saturation. A steepening of the lapse rate in this fashion might produce CAPE in situations where none had previously existed.

Although the terminology ``convective'' instability suggests a close relationship to isolated convective cells,<sup>4</sup> Rossby (1932, p. 26) suggested that layer lifting during ascent over fronts was a possible means to realize convective instability. ``Obviously,'' he stated, ``the nature of convection is not such that a large body of air is lifted solidly to higher levels, but it is equally plain that we can not hope to find a dependable criterion for convection on the highly artificial assumption that one small element at a time is lifted while the rest of the atmosphere remains in equilibrium.'' To avoid misassociations with isolated convection, Hewson (1937), a British meteorologist, coined the term potential instability for the same concept. In Normand (1938, p. 57) and the subsequent discussion (especially by Hewson on p. 66), it appears that the argument over use of the terms convective or potential instability initially was drawn down American versus British lines. The terms now are used interchangeably.

3b  The utility of potential instability

This layer-lifting process, however, is not typically associated with the development of isolated upright deep moist convection. If it were, layer lifting initially would produce stable stratiform clouds, which would then develop into deep moist convection. Although this process does not appear to be acting in isolated convective storms, it does appear to occur in other circumstances. For example, Schultz and Schumacher (1999, section 5a), discuss examples of so-called downscale convective-symmetric instability (Xu 1986) in which the ascent occurring above warm fronts is punctuated with isolated buoyant convective elements [e.g., the warm-frontal elevator/escalator concept of Neiman et al. (1993)]. It is important to recognize that the paths of parcels in such situations are likely to undergo slantwise displacements to their lifting condensation levels (LCL's) and LFC's before releasing the buoyant instability and becoming more upright; this process should be distinguished from slantwise convection due to the release of CSI.

Potential instability is often diagnosed to be present in situations where deep, moist convection is likely, even if the process of convective initiation is not at all related to the layer-lifting process envisioned by Rossby (1932). Not all ``convective'' environments are characterized by the presence of potential (convective) instability, which is a potentially confusing aspect of the term, as noted by Hewson (Normand 1938, p. 66). Generally speaking, the terminology associated with moist instability in the context of gravitational convection is not particularly lucid. Sherwood's comments offer an opportunity to remind ourselves of this. Normand (1938) shows that the concepts associated with conditional instability and its associated metastable state in the presence of CAPE were understood 63 years ago. Regrettably, the clarity of Normand's exposition has not always been manifest in the literature on gravitational convection.

4  Ingredients-based methodology

The ingredients-based methodology states that three ingredients (lift, instability, and moisture) are required for deep, moist convection. Sherwood argues that the ingredient of instability is unfortunately labeled since the three ingredients are actually attempting to diagnose the instability (of which the visible manifestation is deep, moist convection). As we have seen in this paper already, there are numerous problems associated with the meaning and use of the term ``instability.'' The use of the term instability among the ingredients was intended to infer the lapse-rate definition of conditional instability (e.g., Doswell 1987). The three ingredients were chosen (a) to imply the presence of CAPE via conditional instability and moisture, and (b) to realize that convective potential via the ascent of parcels to their LFC's. Clearly, if a sounding has no layer of conditional instability, deep, moist convection is precluded (i.e., there can be no CAPE if lapse rates do not exceed moist adiabatic somewhere in the environmental sounding). The three ingredients are the necessary conditions for the initiation of deep, moist convection and are not intended to diagnose an instability, per se. If CAPE is present and the lift is enough to attain an LFC, then these conditions also become sufficient for deep, moist convection. The ingredients-based methodology does not provide details regarding the distribution of conditionally unstable lapse rates or moisture, because CAPE can be found in vertical soundings under many different circumstances. Thus, we see the success of the energy-based definition for evaluating instability: two of the three ingredients are accounted for in a single combined parameter: either CAPE or potential instability.

Although we have demonstrated problems with the lapse-rate definition, the advantage of the ingredients-based methodology is that the lapse rates and moisture are considered independently. Thus, forecasters anticipating the atmospheric changes allowing deep, moist convection to develop can more easily visualize the destabilizing influences of lapse rate and moisture separately, rather than trying to visualize the processes changing CAPE or potential instability. Therefore, we see no actual disagreement between ourselves and Sherwood in this matter, because the available-energy definition is accounted for by treating the lapse rate and moisture separately in the ingredients-based methodology. Sherwood's comments allow us the opportunity to clarify the intentions of the ingredients-based methodology.

5  Conditional symmetric instability

Analogous to its gravitational counterpart, CSI can be diagnosed in more than one way: the lapse-rate definition of CSI and the available-energy definition of CSI. As discussed in Schultz and Schumacher (1999), the lapse-rate definition of CSI is equivalent to the M_g-q_e^* relationship or negative MPV_g^*, whereas the available-energy definition of CSI is equivalent to SCAPE (slantwise convective available potential energy). Sherwood argues that SCAPE, not MPV_g^*, should be the favored form for diagnosis. Unfortunately, SCAPE has not been found useful in what little available literature has been published (Schultz and Schumacher 1999, section 3d). Thus, Schultz and Schumacher (1999) argued that the most logical and consistent way to diagnose CSI was to locate regions of negative MPV_g^*. There are three possible explanations for this apparent nonutility of SCAPE compared to MPV_g^*.

First, CAPE typically represents available energy through the entire troposphere once the parcel reaches its LFC. The LCL and LFC are usually fairly close to each other in gravitational convection. With SCAPE, however, the vertical extent of the instability is usually much more shallow (less than a couple hundred mb) and the horizontal and vertical distances between the slantwise LCL and slantwise LFC can be much greater. The location of CSI with respect to the location of the lift may be critical because of the typically shallow nature of the instability (and its location far removed from the slantwise LCL). By using MPV_g^*, the spatial relationship between the instability and lift can be visualized. For example, knowledge of the relative locations between the region of MPV_g^* < 0 and the lifting mechanism allows the forecaster to know how strong the lift has to be to reach the instability. Operational experience suggests that a separation of 100 or 200 mb between the region of frontogenesis and the negative MPV_g^* layer implies that a strong frontal circulation is required to access the instability.

Second, the computation and display of SCAPE is problematic. Unlike CAPE, where a single vertically integrated value can be associated with each horizontal location and can be easily displayed on a horizontal map, SCAPE is an integrated quantity along a slantwise path. Thus, what is the best way to display such a quantity? At what horizontal location does it apply?

Third, observed values of SCAPE tend to be relatively small, whereas mesoscale numerical models tend to produce larger values. Perhaps an analogy can be drawn between gravitational and slantwise convection to explain this observation. Before convection starts, soundings in the environment would indicate positive available potential energy. Once convection occurs, soundings taken within storms would indicate little, if any, CAPE/SCAPE. Previous work on SCAPE has focused on the period when slantwise convection is already occurring (e.g., Emanuel 1988). This may explain the absence of SCAPE (i.e., the symmetrically neutral state) in such observational studies. In contrast, mesoscale models typically do not have the resolution or the parameterization to reduce SCAPE (e.g., Schultz and Schumacher 1999, section 7). Therefore, SCAPE may build up to values larger than those observed.

Although Schultz and Schumacher (1999) favored the lapse-rate definition of CSI, further research on different approaches to diagnose the potential for slantwise convection was encouraged. Based on Sherwood's comments and to maintain consistency, SCAPE would appear to be preferred over MPV_g^*. But, as we argued in section 4 for gravitational convection, it may be preferable to consider symmetric lapse rates (via MPV_g^*) separately from moisture for some purposes. Also, research supporting SCAPE as an effective diagnostic tool is lacking, prohibiting us from enthusiastically supporting SCAPE. Previous work by Shutts (1990) and more recent research by Dixon (2000) suggests some utility of SCAPE in numerical models, particularly in anticipating the development of cloud heads in oceanic cyclones. Gray and Thorpe (2000) also reexamine the computation of SCAPE and suggest an alternative method based on trajectories from a mesoscale model. Hopefully, this body of recent research will encourage others to explore techniques for diagnosis and evaluate the utility of SCAPE in a forecasting environment.

6  Conclusion

Although we agree with much of what Sherwood says about the terminology associated with moist gravitational and slantwise convection, this dialog perhaps draws attention away from how to assess the potential for slantwise convection. As stated in Schultz and Schumacher (1999), we feel that if slantwise convection occurs in the atmosphere, then it must be initiated by finite-amplitude disturbances, rather than infinitesimal perturbations. Therefore, an emphasis on instability may distract scientists and forecasters from the real issue: what is the lift mechanism responsible for the precipitation? This question is relevant whether the precipitation is a result of moist gravitational convection, moist slantwise convection, or even stable ascent of moist air. Thus, we wish to emphasize that, in diagnosing precipitation processes, assessing the mechanism for forcing ascent should be the primary concern. The degree of instability (as measured by lapse rate or available energy) merely modulates the response to the forcing.

Finally, the debate between lapse-rate-based and energy-based measures of moist symmetric instability should not detract from the message that scientific debate usually indicates the sign of a healthy discipline. The purpose of the present discussion is to improve the diagnostic methodology, not to invalidate it.

Acknowledgments. We thank Steve Sherwood and Kerry Emanuel for engaging in this dialog with us and providing their feedback. Katherine Day (NOAA Library, Boulder) performed an extensive literature survey on the early history of moist instability and its terminology, initiated by references provided by Leo Donner (NOAA/GFDL, Princeton).

Brooks, H. E., C. A. Doswell III, and J. Cooper, 1994: On the environments of tornadic and nontornadic mesocyclones. Wea. Forecasting, 9, 606-618.

Bryan, G., and J. M. Fritsch, 2000: Moist absolute instability: The sixth static stability state. Bull. Amer. Meteor. Soc., 81, in press.

Dixon, R. S., 2000: Diagnostic studies of symmetric instability. Ph.D Dissertation, University of Reading, 118 pp. [Available from Department of Meteorology, University of Reading, Earley Gate, PO Box 243, Reading RG6 6BB, United Kingdom.]

Doswell, C. A. III, 1987: The distinction between large-scale and mesoscale contribution to severe convection: A case study example. Wea. Forecasting, 2, 3-16.

Emanuel, K. A., 1988: Observational evidence of slantwise convective adjustment. Mon. Wea. Rev., 116, 1805-1816.

Emanuel, K. A., 1994: Atmospheric Convection. Oxford University Press, 580 pp.

Emanuel, K. A., 1997: Overview of atmospheric convection. The Physics and Parameterization of Moist Atmospheric Convection, R. K. Smith, Ed., Kluwer, 1-28.

Gray, S. L., and A. J. Thorpe, 2000: Parcel theory in three-dimensions and the calculation of SCAPE. submitted to Mon. Wea. Rev.

Hess, S. L., 1959: Introduction to Theoretical Meteorology. Holt-Dryden, 362 pp.

Hewson, E. W., 1937: The application of wet-bulb potential temperature to air mass analysis. III  Rainfall in depressions. Quart. J. Roy. Meteor. Soc., 63, 323-337.

Johns, R. H., and C. A. Doswell III, 1992: Severe local storms forecasting. Wea. Forecasting, 7, 588-612.

Kain, J. S., and J. M. Fritsch, 1998: Multiscale convective overturning in mesoscale convective systems: Reconciling observations, simulations, and theory. Mon. Wea. Rev., 126, 2254-2273.

Kutzbach, G., 1979: The Thermal Theory of Cyclones. Amer. Meteor. Soc., 255 pp.

McNulty, R. P., 1978: On upper tropospheric kinematics and severe weather occurrence. Mon. Wea. Rev., 106, 662-672.

McNulty, R. P., 1995: Severe and convective weather: A Central Region forecasting challenge. Wea. Forecasting, 10, 187-202.

Moncrieff, M. W., and M. J. Miller, 1976: The dynamics and simulation of tropical cumulonimbus and squall lines. Quart. J. Roy. Meteor. Soc., 102, 373-394.

Neiman, P. J., M. A. Shapiro, and L. S. Fedor, 1993: The life cycle of an extratropical marine cyclone. Part II: Mesoscale structure and diagnostics. Mon. Wea. Rev., 121, 2177-2199.

Normand, C. W. B., 1931a: Graphical indication of humidity in the upper air. Nature, 128, 583.

Normand, C. W. B., 1931b: Recent investigations on structure and movement of tropical storms in Indian Seas. Gerlands Beitr., 34, 233-243.

Normand, C. W. B., 1938: On instability from water vapour. Quart. J. Roy. Meteor. Soc., 64, 47-69.

Peslin, H., 1868: Sur les mouvements généraux de l'atmosphère, Bull. Hebd. l'Ass. Sci. France, 3, 299-319.

Petterssen, S., 1956: Weather Analysis and Forecasting, Vol. 2, Weather and Weather Systems. 2nd ed., McGraw-Hill, 266 pp.

Refsdal, A., 1930: Der feuchtlabile Niederschlag. Geofys. Publ., 5(12), 1-71.

Reye, T., 1864: Ueber vertikale Luftströme in der Atmosphäre. Zeits. für Mathematik und Physik, 9, 250-276.

Rossby, C.-G., 1932: Thermodynamics applied to air analysis. MIT Meteorological Papers, 1(3), 31-48, plus 11 plates.

Schultz, D. M., and P. N. Schumacher, 1999: The use and misuse of conditional symmetric instability. Mon. Wea. Rev., 127, 2709-2732; Corrigendum, 128, 1573.

Shaw, N., 1926: Manual of Meteorology, Vol. I, Cambridge University Press. 339 pp.

Sherwood, S. C., 2000: On moist instability. Mon. Wea. Rev., 128, 4139-4142.

Shutts, G. J., 1990: SCAPE charts from numerical weather prediction model fields. Mon. Wea. Rev., 118, 2745-2751.

Sohoni, V. V., and M. M. Paranjpe, 1937: Latent instability in the atmosphere revealed by some Indian tephigrams. Mem. India Met. Dept., 26, 131-149, plus 10 plates.

Xu, Q., 1986: Conditional symmetric instability and mesoscale rainbands. Quart. J. Roy. Meteor. Soc., 112, 315-334.

Footnotes:

¹ Although the term CAPE would not be coined until Moncrieff and Miller (1976), the concept of available energy had been discussed previously. In this paper, we define CIN as the negative area/energy on a thermodynamic diagram and CAPE as the positive area, in contrast to Emanuel (1994, p. 171) where CAPE is the difference between the positive and negative areas.

² Neglecting terms nonlinear in z requires that gz/T₀ << 1. If z = 3 km, this approximation will err by only about 10%.

³ It can be shown that, in order to neglect the nonlinear terms in the Taylor expansion (2), g >> ¹/₂z[(d g)/ dz] must occur. In other words, the change in environmental lapse rate over z is small compared to the environmental lapse rate. If g were constant with height, the linearized Taylor expansion would be exact.

⁴ During the time that Rossby defined convective instability (1932), the term ``convective'' was often used in the same way as ``advective'' is used today. Such a tradition continues today in some branches of fluid dynamics. It was likely that Rossby innocently used convective in that sense (K. Emanuel 2000, personal communication). Of course, this in no way changes the fact that the terminology can be very misleading today.