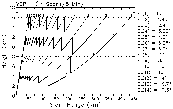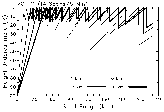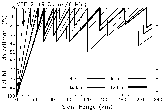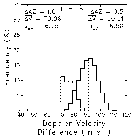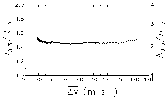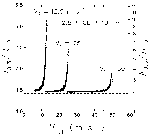Development of New WSR-88D Scanning Strategies
for Convective Situations

Rodger A. Brown and Vincent T. Wood
National Severe Storms Laboratory
Norman, OK

Final Report

Task 8.2

1998 Memorandum of Understanding Between
WSR-88D Operational Support Facility
and
National Severe Storms Laboratory

January 1999

http://www.nssl.noaa.gov/~wood/OSF_MOU/CY98/Task8.2/FinalReport.html

1. Introduction

The purpose of this report is to discuss the development of new WSR-88D scanning strategies, or Volume Coverage Patterns (VCPs), in response to needs expressed by WSR-88D users. These new strategies are relatively long-term solutions, because most of the algorithms need to be modified in order to accommodate the proposed changes.

In preparation for producing new VCPs, we developed a technique that creates "optimized" VCPs. That is, we create a set of elevation angles that produces maximum height uncertainties that are comparable at all ranges from a radar. In this way, maximum uncertainties in the height of a storm or other feature will be the same no matter how far it is from a given radar.

The needs for new VCPs expressed by various users fall into three main categories: (1) need for improved vertical resolution, (2) need for improved temporal resolution and (3) need for improved horizontal resolution. We have not addressed the special needs of WSR-88Ds located on mountain tops, because they will be resolved in a follow-on study. Listed below are representative comments received from the users.

Comments related to the need for improved vertical resolution:

* supercell storms and their embedded mesocyclones are difficult to observe at long ranges

* mini-supercell storms and their embedded mesocyclones are difficult to observe at moderate to long ranges

* since lake-effect storms are shallow, the radar beam cuts through the top of the clouds at a range too close to the radar

* tornadic circulations in hurricanes are shallow

* precipitation in hurricanes is hard to estimate because of the high shear and shallow nature of the storms

* precipitation in winter storms is hard to estimate owing to the shallow nature of the storms

* precipitation measurements in high precipitation events may be improved by changing the VCP

* a large "cone of silence" decreases radar coverage when the radar is located in a heavily populated area

Comments related to the need for improved temporal resolution:

* tornadoes in supercell storms develop and evolve very quickly, faster than current volume scans are updated

* microbursts form quicker than volume scans are updated

* tornadic circulations in hurricanes spin up very quickly

* nonsupercell tornadoes are shallow and spin up very quickly

Comments related to the need for improved horizontal resolution:

* supercell storms and their embedded mesocyclones are difficult to observe at long ranges

* mini-supercell storms and their embedded mesocyclones are difficult to observe at moderate to long ranges

* tornadic circulations are not easily resolved, especially at longer ranges

We kept these needs in mind when we developed the new set of VCPs. In section 2, we point out some inherent problems with current VCPs 11 and 21. In section 3, we develop a technique for optimizing the distribution of elevation angles within a VCP. In section 4, we develop a set of VCPs that satisfy the users' needs for improved vertical and temporal resolution. In section 5, we propose a solution for the horizontal resolution problem. In section 6, we look at the case for lowering the lowest elevation angle to 0.3o. Our recommendations are summarized in section 7.

2. Characteristics of VCP 11 and VCP 21

Currently, there are two VCPs that are used for the detection of convective storms. VCP 11 consists of 14 elevation scans (0.5-19.5o) in 5 min and VCP 21 consists of 9 scans (also 0.5-19.5o) in 6 min. Plotted in Figs. 1 and 2 are the VCPs and corresponding height underestimates associated with them (analogous to figures used by Howard et al. 1997). As an example of how to interpret the colored bands in the figures, assume that VCP 11 (Fig. 1) is used to detect the top of a 15-km-tall storm at a range of 230 km. Storm top is above 2.4o elevation, but below 3.35o elevation. The highest elevation angle showing radar return is 2.4o, which represents a height of 13 km at 230 km range. The boundary between the yellow and red bands at 15-km height indicates that the radar underestimates storm top by 2 km, yielding an apparent storm top of 13 km.

Fig. 1. Height of VCP 11's elevation angles as a function of slant range. The center of the radar beam lies along the labeled line (boundary between red and green). The height of a storm feature that lies between two elevation is determined by the lower elevation angle and therefore is underestimated by the amount indicated by the colored bands. Fig. 2. Same as Fig. 1, except for VCP 21.

VCP 11 and 21 have five common elevation angles up through 4.3o. The spacing between the angles is so coarse that the WSR-88D does a poor job in resolving mid- and upper-altitude features at far range. VCP 21 (Fig. 2) does an extremely poor job in resolving mid- and upper-altitude features at all ranges. The height underestimates are presented in a different form in Figs. 3 and 4 (analogous to figures used by Maddox et al. 1999). The dotted horizontal lines in the figures represent storm features at 4, 8, 12 and 16 km heights. The jagged line at a given height represents the variation of apparent height (that is, highest elevation angle with radar return) as the radar scans upward through that height. The curves for VCP 11 (Fig. 3) show increasing underestimation with increasing range from the radar. The curves for VCP 21 (Fig. 4) show almost random variation with range owing to the irregular and large spacing between elevation angles.

Fig. 3. Variation of the apparent height of a storm feature as a function of range for VCP 11. The dotted horizontal line shows the true height of a feature and the jagged line shows the apparent height measured by the radar. The elevation tilts are labeled 1-14 and are identified on the right side of the figure. Fig. 4. Same as Fig. 3, except for VCP 21.

One may note, especially in Fig. 3, that the amount of variation increases nearly linearly with height. This finding suggests that height variation expressed as a fraction of the true height (the dotted lines) is essentially independent of height. To test this idea, the variations in the curves in Figs. 3 and 4 were replotted in Figs. 5 and 6 as a percentage of the true height. Except for variations attributable to the lower elevation angles, the maximum height underestimation, expressed in percentage, is about the same. Beyond 150 km, the curves for VCP 11 and 21 are the same because the lowest five elevation angles are the same for both VCPs.

Fig. 5. Replotting of the jagged curves from Fig. 3 as normalized curves (VCP 11). The height of each jagged curve is expressed as a percent height uncertainty relative to the true height indicated by the respective dotted line in Fig. 3.

 Fig. 6. Same as Fig. 5, except for VCP 21.

3. Technique for optimizing VCPs

The relative consistency of the curves in Figs. 5 and 6 inspired us to develop a new technique for designing new VCPs. The approach is to specify the maximum height uncertainty desired (expressed as a percentage) and then compute the set of elevation angles that satisfy that constraint. The process involved is illustrated in Fig. 7. First, one specifies a true height (Zt); we chose a height of 10 km because it represents a middle height for convective storms. Then one specifies a maximum height underestimate (H%) as a percentage of Zt. Finally, one specifies the minimum elevation angle (Elk) and maximum elevation angle. Though a lower minimum elevation angle is desirable (see section 6), we chose the current value of 0.5o for the minimum angle. Since the WSR-88D was designed with a mechanical stop at 60o elevation, we specified the maximum elevation angle to be 58o. One needs the higher elevation angles to document storm evolution over populated areas close to the radar.

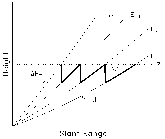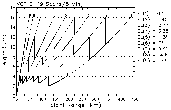
Fig. 7. Schematic of the process used to compute optimized VCPs. See discussion in the text for details.

The procedure (as shown in Fig. 7) is to start at the slant range where the lowest elevation angle is equal to Zt (right edge of the figure). With decreasing slant range (rs) at that elevation angle, one computes the height underestimate (Z = Zt - h). When Z equals H% , one jumps back up to Zt and computes the elevation angle (Elk+1) that corresponds to that slant range and Zt. Then one repeats the process until the new Z equals H%. In this way, one develops a VCP that has a consistent maximum height underestimate.

We computed the elevation angles and cumulative scan times for 16 potential VCPs having maximum height underestimates ranging from 15 to 30%. For these new VCPs, we used maximum reasonable rotation rates as determined by Dale Sirmans. For elevation angles below 1.45o, the radar makes two complete scans at each elevation angle. There the rotation rate was 3.5 rpm for the contiguous surveillance (CS) mode and 4.0 rpm for the contiguous Doppler (CD) mode. For the batch mode between elevation angles of 1.45 and 7.0o, the rotation rate was 4.5 rpm. For the CD mode at 7.0o and above, the rotation rate was 4.8 rpm. We approximated the time it takes (a) for the antenna to rise to the next elevation angle and (b) for the various computations that are made as the antenna descends at the end of the volume scan by multiplying the elevation angle increment between scans by 1.3 s deg-1. By prorating the time for descent and finishing computations to each elevation scan, we have a reasonable estimate of how long a volume scan will take if the scan ends after an arbitrary number of tilts.

Listed in Table 1 are the elevation angles and cumulative scan times (minutes and seconds) for 16 potential VCPs; plots of the data are shown in Figs. 8 and 9. The jump in the time curves in Fig. 8 between maximum height underestimates of 21 and 22% is due to the fact that the number of elevation angles below 1.45o decreased from three to two. For a maximum height underestimate of 15%, there are 23 scans in 6.9 min, reaching an elevation angle of 47.2o. At the other extreme, for 30%, there are 11 scans in 4.0 min, reaching an elevation angle of 44.5o. The transition from 15% to 30% is so gradual that it is difficult to choose specific VCPs.

Fig. 8. Plots of volume scan times from Table 1 as a function of the number of elevation tilts for a number of flexible VCPs represented by various maximum height underestimates. Fig. 9. Plots of elevation angles from Table 1 as a function of the number of elevation tilts for a number of flexible VCPs represented by various maximum height underestimates.

As an example of the advantages of the optimization technique, we produced optimized versions of VCP 11 and 21. We kept the same lowest and highest elevation angles and the same number of elevation scans as in the original VCPs. The faster rotation rates used to compute the numbers in Table 1 were not taken into account for this example. The optimized version of VCP 11 (Fig. 10) had a maximum height underestimate of 19.38%. As one may note in Fig. 10, the maximum height underestimate is not quite uniform with range as the height departs from the computation height of 10 km. An optimized version of Fig. 1 is shown in Fig. 11. The optimized VCP provides better low elevation coverage at far ranges. Also, the more uniform distribution at higher elevation angles is quite evident. Clearly this optimization approach produces superior VCPs.

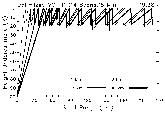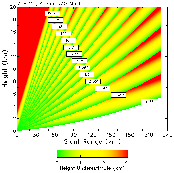
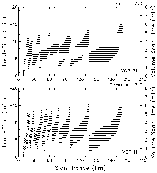
Fig. 10. Same as Fig. 5, except for optimized VCP 11. Fig. 11. Same as Fig. 1, except for optimized VCP 11.

4. VCPs having improved vertical and temporal resolution

a. Strategies for new VCPs

The data in Table 1 provide a family of potential new VCPs that have the types of improved vertical and temporal resolution that users have been requesting. The problem is to decide which ones to use. Before we proceed, however, we want to establish the difference between flexible and inflexible VCPs. An inflexible VCP is like the ones currently in use with the WSR-88D. Once the VCP is selected, it sequences through a set of elevation angles in a fixed amount of time. It doesn't matter whether there are storms at far range where there are no echoes above 7o elevation or whether storms are passing over the radar. On the other hand, a flexible VCP allows an algorithm to specify when the VCP should end and start a new cycle. An algorithm would determine when there have been two successive scans with no radar return present. When that occurs, the volume scan automatically ends. A new volume scan begins as soon as the antenna returns to the lowest elevation angle and the end-of-volume-scan computations are completed. This approach was used successfully in the 1970s and 1980s for selected WSR-57 radars as part of D/RADEX (e.g., Saffle 1976) and RADAP II (e.g., Greene et al. 1983).

Temporal resolution is improved using a flexible VCP. Also, the increased rotation rates incorporated into Table 1 help to improve the temporal resolution. Considering these capabilities for improving temporal resolution, we are ready to zero in on a couple of VCPs that improve vertical resolution.

b. Development of VCP A

Since optimized VCP 11 has a maximum height underestimate of 19.38%, it would be good to select a VCP that has greater vertical resolution. At the same time, we don't want the vertical resolution to be so great that the average elevation increment between the lowest 4 to 6 elevation angles is much less than half the vertical beamwidth (that is, less than about 0.45-0.5o). The VCP having a maximum height underestimate of 18% fits these requirements. We call this VCP A and it is plotted in Fig. 12. Figure 13 shows plots of the maximum height underestimates.

VCP A completes 19 scans in about 6 min and goes to an elevation angle of 46.6o (18% in Table 1). This VCP helps to satisfy the users' need for a reduced "cone of silence" to detect reflectivity features near the radar. Tall storms as close as about 15 km to the radar are covered to storm top. With flexible capability, the radar completes 16 scans in 5 min and reaches an elevation angle of 23.6o. Tall storms as close as 25-35 km to the radar are covered to storm top with the 5-min sampling; minisupercells as close as 20 km are covered. In 3.5 min, the radar completes 11 scans and reaches an elevation angle of 8.4o. With 3.5-min sampling, rapidly-evolving features in the lowest 3 km are covered as close as 20 km to the radar.

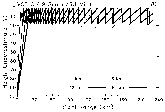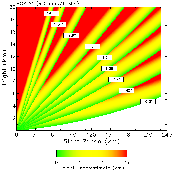
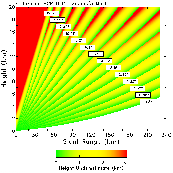
Fig. 12. Same as Fig. 1, except for optimized VCP A. Fig. 13. Same as Fig. 5, except for VCP A.

Besides the decreased cone of silence at near range, another advantage of VCP A is the increased vertical resolution at moderate to far ranges. Within the lowest 6o of elevation, VCP A has 9 scans, compared to 6 for both VCPs 11 and 21. Within the lowest 3o, the average increment between elevation angles is 0.47o, compared with 0.95o for VCPs 11 and 21. The increased rotational speed of the radar's antenna makes possible the increased vertical resolution at all ranges.

c. Development of VCP B

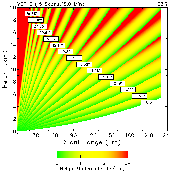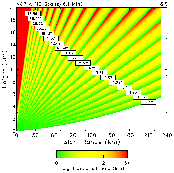
It would be helpful to have a second VCP that, during the same time interval, scans twice as high as VCP A. Such a VCP is one that has a maximum height underestimate of 23%. We call this one VCP B. Its elevation angles are plotted in Fig. 14. The corresponding maximum height underestimates are plotted in Fig. 15.

Fig. 14. Same as Fig. 1, except for optimized VCP B. Fig. 15. Same as Fig. 5, except for VCP B.

VCP B completes 15 scans in 5 min and goes to an elevation angle of 51.6o (Table 1). This VCP also helps to satisfy the users' need for a reduced "cone of silence" near the radar. As with VCP A, this VCP scans to the top of tall storms that are as close as 15 km to the radar. The vertical resolution of VCP B is coarser than that for VCP A and accordingly completes the full scan in 5 min instead of 6 min. This flexible VCP scans to 20.9o in 3.7 min, compared to 19.5o in 5 and 6 min for VCPs 11 and 21, respectively. This VCP is the preferred one to use for rapidly-evolving shallow phenomena. For example, the radar can sample phenomena as close as 15-20 km every 3.5 min if the phenomena are 5-km deep and every 3 min if they are 3-km deep. The lowest elevation angle of 0.5o limits far-range detection of shallow phenomena.

VCPs A and B satisfy the needs expressed in the Introduction. They allow better vertical and temporal resolution of long-range features. They also allow better vertical and temporal resolution of shallow phenomena at close and moderate ranges from a radar. The improved vertical resolution permits better estimation of precipitation in shallow storms, such as hurricanes and winter storms. They allow better documentation of rapidly evolving features, such as tornadoes and downbursts. They decrease the "cone of silence", allowing the radar to detect phenomena over populated areas located close to the radar.

d. Testing improved vertical resolution

Vertically integrated liquid (VIL) is a computed quantity that forecasters use to estimate the severity of a storm. It is a measure of the liquid water in a vertical column in the storm and is computed as a function of the vertical profile of reflectivity (Greene and Clark 1972). Owing to its vertically integrated properties, we use VIL as a means for comparing the vertical resolution of the various VCPs.

We used a vertical profile of maximum reflectivity within an individual convective cell to compute VIL; VIL computed in this manner is called "cell-based VIL". The profile was derived from the composite time-height evolution shown in Fig. 16. We based the composite on (a) data presented by Kingsmill and Wakimoto (1991) from an Alabama hail- and microburst-producing multicell storm and (b) data presented by Torgerson and Brown (1996) from a North Dakota hail-producing multicell storm. VIL was computed from the reflectivity profile at 20 min shown in Fig. 16. The true value of VIL, computed using z values of 0.1 km, is 80.5 kg m-2.

Fig. 16. Schematic time-height plot of maximum reflectivity within a cell of a multicell storm. The schematic is based on a composite of data from an Alabama hail- and microburst-producing multicell storm (Kingsmill and Wakimoto 1991) and a North Dakota hail-producing multicell storm (Torgerson and Brown 1996).

Figure 17 contains VIL values plotted as a function of range for VCPs 11 and 21, optimized VCP 11 and VCPs A and B. The VIL values based on VCP 21 are much more erratic than those for the other VCPs, fluctuating by up to 12-14 kg m-2 from the true value. Mahoney and Schaar (1993) also pointed out the erratic behavior of VIL based on VCP 21. Within about 110 km of the radar, the VIL values for the other VCPs all fluctuate from -2 to +4 kg m-2 of the true value. At closer range, owing to the decreased "cone of silence" associated with VCPs A and B, realistic VIL values are computed to within 15 km of the radar as opposed to 30-35 km for the other VCPs.

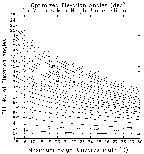
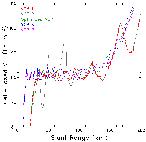
The increase in unrealistic VIL values beyond about 110 km is a consequence of the vertical distance between elevation angles which increased with range. As part of the vertical integration process, the maximum reflectivity within the storm at each elevation angle is assigned to a depth (z) extending from halfway to the adjacent lower elevation angle to halfway to the adjacent higher elevation angle. So, as z increases with range, the height interval containing the largest reflectivity values carries an increasing amount of weight in computing the VIL value. Beyond about 125 km, the VCP 11 (red x) and VCP 21 (gray line) curves coincide because most of storm depth is below 5.25o, where elevation angles are the same.

We also computed VIL for a cell that had half the height and time extent of the one shown in Fig. 16; reflectivity values remained the same. Figure 18 shows the resulting cell-based VIL values. The true VIL value is 40.2 kg m-2, one-half of that for the taller cell. The fluctuations also are about half of those for the taller cell. The decrease in values beyond 160 km is because there are, at most, only two or three elevation angles within storm depth.

Fig. 17. Vertically integrated liquid computed as a function of range from the reflectivity composite in Fig. 16. The vertical reflectivity profile at 20 min was used for the computations. The horizontal line is the true VIL value of 80.5 kg m-2. VCP 11 is indicated by red Xs.

Fig. 18. Vertically integrated liquid computed as a function of range from a reflectivity composite. The composite had half the height scale and half the time scale of the one in Fig. 16. The vertical reflectivity profile at 10 min (comparable to 20 min in Fig. 16) was used for the computations. The horizontal line is the true VIL value of 40.2 kg m-2. VCP 11 is indicated by red Xs.

In summary, VCPs A and B (and the optimized version of VCP 11) produce more consistent values of VIL over a wider range interval than do VCPs 11 and 21. The taller the storm, the greater the range from the radar where realistic values are found.

e. Testing improved temporal resolution

One of the severe storm events that has a short lead-time is the downburst. A Damaging Downburst Prediction and Detection Algorithm is being developed at the present time at NSSL. However, the WSR-88D data set upon which the selection of significant parameters and their threshold values will be based is still being accumulated. In their study of microbursts (small-scale downbursts) in Colorado, Roberts and Wilson (1989) found that descending maximum reflectivity cores associated with midaltitude convergence are good indicators of a developing microburst. These signatures appeared 0-10 min before outflow winds occurred at the surface.

To develop a downburst model, we used the same time-height profile of maximum reflectivity that was used for VIL computations (Fig. 16). Since we do not have midaltitude convergence information available, we simply used descent of the reflectivity core as the precursor signature of a downburst. Without much guidance to go by, we arbitrarily assumed that the precursor signature for a downburst was the first detection of a descent rate greater than 3 m s-1.

Using VCPs 11, 21, A and B, we computed the lead-time as a function of range. We defined lead-time as the time difference between the time the precursor signature was first detected and 32.0 min (the assumed time of significant downburst development based on core descent in Fig. 16). For flexible VCPs A and B, we assumed that the volume scan ended at the end of the first elevation scan above 16 km height. The random temporal placement of a volume scan relative to the reflectivity features affects the value of the computed descent rate. To take into account the various random placements, we divided the time interval between volume scans into ten equal parts and computed 9 additional lead-times, each successively offset in time by one tenth of the volume scan time interval.

Figure 19 shows the resulting lead-times as a function of range for VCPs 11 and 21. The 10 dots or horizontal lines at each range represent the 10 offset estimates of lead-time for one volume scan. The thick line indicates the same time interval between volume scans at all ranges. There are no lead-times beyond 200 km owing to the lowest elevation angle being too high in the storm to detect the descent. The abrupt changes in lead-time as a function of range arise from the placement and vertical separation of the elevation angles relative to the height of the maximum reflectivities in the core region. Each segment in the figure represents a given pair of elevation angles between which the descent rate was computed. The variation in lead-time at a given range, owing to the random location of a volume scan relative to the reflectivity core, is about 5.5 min for VCP 21 and 4.5 min for VCP 11. The slightly smaller variation for VCP 11 probably is due to the shorter time interval between volume scans.

Fig. 19. Downburst lead-times as a function of slant range for the reflectivity composite in Fig. 16 using VCP 21 (top) and VCP 11 (bottom). The 10 dots or horizontal lines at each range represent the 10 lead-times that were computed from a set of volume scans that were offset from each other by one-tenth the time interval between volume scans. The set of 10 offset scans is a proxy for all of the possible random placements of volume scans relative to the reflectivity core region. The thick line indicates the time it takes to complete one volume scan (scale on the right).

Fig. 20. Same as Fig. 19, except for VCP A (top) and VCP B (bottom).

Figure 20 shows the lead-times for optimized VCPs A and B. Being flexible VCPs, the time to complete a volume scan decreases with range because there are a decreasing number of elevation scans within the storm depth. One notes that, as the volume scan time decreases, the minimum lead-time increases slightly and exhibits decreasing variation among the 10 offset volume scans at each range; had the VCPs been inflexible (that is, each volume scan went to the highest elevation angle), both the minimum lead-time and the variation among the 10 offset volume scans would have remained essentially unchanged with increasing range. The variations among the 10 offset scans for VCP A decrease from about 5.5 min at close range to 2.5 min at far range. Similar variations for VCP B decrease from about 4.5 min at close range to 2 min at far range. The data presented in Figs. 19 and 20 clearly indicate that the average downburst lead-times significantly increase at farther ranges with the reduced volume scan times that are possible with a flexible VCP.

5. Improving horizontal resolution

Users have documented their frustrations in trying to detect tornadoes and far-range mesocyclones using the WSR-88D. The problems arise owing to the broadening of the radar beam with range and to the 1.0o incremental collection of data in the azimuthal scanning direction. One could decrease the rate of beam broadening with range by increasing the size of the antenna or decreasing the transmitted wavelength. Neither of these options is feasible. However, something can be done about the azimuthal data collection interval. One could decrease the azimuthal data collection increment to 0.5o by cutting the antenna rotation rate in half, cutting the number of pulses in half or by doing some combinations of these two approaches. Cutting the rotation rate in half would be counterproductive, because that would decrease the temporal resolution. Cutting the number of pulses in half is feasible as long as there are enough pulses to compute reliable reflectivity, mean Doppler velocity and spectrum width values.

Using analytical simulations, Wood and Brown (1998) and Brown and Wood (1998) have shown that mesocyclone and tornado detection, respectively, can be noticeably improved by cutting the number of pulses in half while maintaining the usual VCP 11 and 21 rotation rates. For their simulations, they use the Rankine combined vortex model. The Rankine combined vortex consists of a solidly-rotating core where the rotational velocity increases linearly from zero at the vortex center to the maximum value at the edge of the core. Outside the core region, the rotational velocity decreases inversely proportionally to distance from the center of the vortex.

When a simulated radar scans past the model vortex, the averaging that takes place across the radar beam degrades the vortex signature to some extent. Because a mesocyclone is significantly wider than the radar beam, serious degradation takes place only at far ranges. However, a tornado is smaller than the radar beam at all ranges, except within a few kilometers of the radar. Brown et al. (1978) refer to Doppler velocity measurements across a tornado as a tornadic vortex signature (TVS). They called the signature a TVS instead of a tornado signature because, at most ranges, the peak Doppler velocity values are so degraded that they bear no resemblance to the actual size or strength of the tornado. The peak Doppler velocities in a TVS are about one beamwidth apart, regardless of tornado size or strength. The TVS is a prominent Doppler velocity feature that forecasters use to indicate the presence of a tornadic circulation.

a. Improved tornado detection

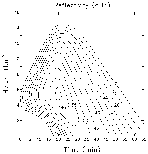
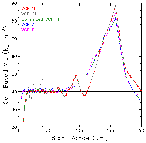
Using the Rankine combined vortex model and a simulated Doppler radar (e.g., Wood and Brown 1997), we produced simulated WSR-88D data for both 1.0o and 0.5o azimuthal increments (AZ). The Rankine model of the tornado had peak rotational velocities of 100 m s-1 at a core radius of 250 m. Figure 21 shows comparisons of simulated TVSs at a range of 50 km from the radar for the two azimuthal increments. The pointed curve is the original Rankine vortex. Owing to the radar beam being considerably wider than the vortex, the data points lie along a degraded TVS curve, where the peak values are significantly less than 100 m s-1 (velocity differences between peaks are significantly less than 200 m s-1). With 1.0o azimuthal increments (Fig. 21a), the Doppler velocity difference between the peaks of the TVS curve is 82 m s-1. The placement of data points along the TVS curve varies from one radar scan to the next past the tornado. Here, the velocity difference between the extreme data points (V) is 65.0 m s-1. The Doppler velocity difference varies from scan to scan, depending on where the data points fall relative to the peaks of the TVS curve.

Figure 21b shows the situation for 0.5o azimuthal increments. Obviously, with closer data spacing, there is a better chance for the data points to be closer to the peaks of the TVS curve. Here, the velocity difference between the extreme data points is 83.2 m s-1 -- an improvement from 65.0 m s-1 with 1.0o AZ. However, there also is a less obvious improvement with 0.5o AZ. The horizontal beamwidth is effectively broadened when the antenna moves a significant amount while the required number of pulses are being transmitted. Since 0.5o azimuthal sampling uses half the number of pulses compared with 1.0o sampling, the nominal effective beamwidth decreases from 1.29o for 1.0o AZ to 1.02o for 0.5o AZ. With a smaller effective beamwidth, there is less degradation of the vortex. Consequently, the velocity difference between the peaks of the TVS curve increased from 82 m s-1 for 1.0o increments to 95 m s-1 for 0.5o increments.

Fig. 21. Example of simulated TVS data points along degraded TVS curves for (a) 1.0o and (b) 0.5o azimuthal sampling (AZ) at a range of 50 km from the radar. The pointed curve represents the tornado being sampled (peak rotational velocity of 100 m s-1 at a core radius of 250 m). The Doppler velocity difference (V) between the extreme positive and negative data points is a measure of the TVS.

With a given tornado at progressively farther distances from the radar, the TVS is progressively degraded because the linear width of the radar beam increases with range. Figure 22 shows an example of the degradation with range for 1.0o and 0.5o increments. At a given range from the radar, the broad bands indicate the spread of V measurements that are likely to occur for (a) the various possible locations of the radar beam relative to the tornado and (b) the addition of Gaussian-distributed white noise (mean of zero) to the Doppler velocity computations to simulate the noisiness in Doppler velocity measurements. When one decreases the number of pulses by a factor of 2 to produce 0.5o azimuthal sampling intervals, the noisiness or standard deviation of the Doppler velocity estimates increases by the square root of 2 (that is, by a factor of 1.4). For the conventional 1.0o azimuthal sampling, the standard deviation is about 2.5 m s-1. For the proposed 0.5o azimuthal sampling, the standard deviation increases to 3.5 m s-1.

Fig. 22. Distribution of TVS Doppler velocity differences (V) as a function of range and azimuthal sampling (AZ) for the tornado specified in Fig. 21. The shaded band represents V values arising from the random placement of the radar beam relative to the center of the tornado; Gaussian distributed noise was added to the individual Doppler velocity data points before V was computed. The solid line is the mean V at a given range and the dotted line is the mean V for the other AZ.

The solid line along the middle of each band in Fig. 22 represents the average of 121 estimates of V at each radar range. The V estimates represent 121 different placements of the vortex center relative to the beam center over one AZ interval. The dotted line represents the location of the solid line in the other half of the figure. It is clear from Fig. 22 that, for the given tornado at a given range, the radar measured a stronger Doppler velocity difference with 0.5o AZ than with 1.0o AZ. On the average, the difference between the two curves is 10-20 m s-1.

Figure 23 shows the distributions of V across the two bands at a range of 50 km from the radar. The mean value of V is 21 m s-1 stronger with 0.5o AZ. One sees that most of the possible V values occur near the center of the bands with fewer occurring at the edges. Contrary to what one might infer from the shaded bands in Fig. 22, only a small fraction of the possible V values in the two distributions actually overlaps.

Fig. 23. Frequency distributions of TVS Doppler velocity differences (V) across the bands at 50 km range in Fig. 22. These distributions are based on 1001 uniformly-spaced radar beam positions ranging from 0.5 AZ to the left of the tornado center to 0.5 AZ to the right. The thin (thick) lines correspond to the 1.0o (0.5o) azimuthal sampling interval. The mean (overbar; vertical dotted line) and standard deviation (s) of each V distribution is indicated.

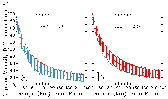
It is common to use threshold values to decide whether a particular V value is strong enough to represent a TVS. Using the mean curves in Fig. 22, it is possible to select a V threshold value and determine how much farther in range one can detect values greater than or equal to the threshold value. For example, a threshold velocity difference of 40 m s-1 occurs at a range of 102 km for 1.0o AZ, while it occurs at a range of 150 km for 0.5o AZ; 150 km is 1.47 times farther in range than 102 km. Plotted in Fig. 24 are the ratios of maximum range at which a particular V value can be detected using 0.5o AZ relative to the maximum range using 1.0o AZ. The ratios occur in a narrow band from 1.45 to 1.55 for all V thresholds. This means that one can detect a particular V threshold at 45-55% greater distances on the average using 0.5o azimuthal sampling. In terms of horizontal coverage, the area exceeding a particular threshold value is doubled on the average using 0.5o azimuthal sampling, which is very significant from an operational perspective.

Fig. 24. Ratios of the range (R) using 0.5o azimuthal sampling to the range using 1.0o sampling for mean V values shown in Fig. 22. The corresponding ratio of coverage areas (A) is indicated along the right edge of the figure.

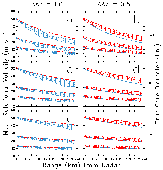
b. Improved mesocyclone detection

We also used the Rankine combined vortex model to simulate mesocyclones. A typical mesocyclone has a peak rotational velocity of 25 m s-1 at a core diameter of 5 km. Figure 25 shows an example of Doppler velocity measurements in such a mesocyclone at a range of 150 km. As with the TVS in Fig. 21, the denser data points with 0.5o AZ do a much better job than 1.0o AZ in representing the peaks of the mesocyclone curve. Also, with a smaller effective beamwidth, the peaks of the mesocyclone curve are closer to the model peaks of 25 m s-1 with 0.5o azimuthal sampling.

Fig. 25. Example of simulated mesocyclone signature data points along degraded mesocyclone signature curves for (a) 1.0o and (b) 0.5o azimuthal sampling (AZ) at a range of 150 km from the radar. The pointed curve represents the true mesocyclone being sampled (peak rotational velocity of 25 m s-1 at a shaded core radius of 2.5 km). Deduced values of the mean rotational velocity (Vrot with overbar; computed as the mean of the extreme positive and negative Doppler velocity data points) in m s-1 and core diameter (CD) in km are indicated.

We simulated nine different mesocyclones to study the improvements associated with 0.5o azimuthal sampling. Three peak velocities (12.5, 25 and 50 m s-1) and three core diameters (2.5, 5 and 10 km) were chosen. Figure 26 shows the resulting velocity bands as a function of range. Again, the dotted lines are used to denote the average center line for the other azimuthal increment. The ratio of ranges for various threshold values is shown in Fig. 27. For a given peak velocity, the ratios associated with the three core diameters successively overlapped to produce one continuous curve. For most threshold values, the ratios were between 1.45 and 1.5. As the threshold value approached the peak velocity value (that is, as range from the radar approached zero in Fig. 26), the ratio increased. This increase is a consequence of the denominator approaching zero faster than the numerator. All of the ratios are above the dashed line that indicates a doubling of the horizontal area of coverage relative to any rotational velocity threshold.

Fig. 26. Same as Fig. 22, except for mean rotational velocities for Doppler velocity signatures of mesocyclones having peak rotational velocities of 12.5, 25 and 50 m s-1 (the three curves in each part of the figure) and core diameters of 2.5 (a, b), 5 (c, d) and 10 km (e, f).

Fig. 27. Same as Fig. 24, except for mesocyclones having peak rotational velocities (Vx) of 12.5, 25 and 50 m s-1. Each curve is the blending of curves for mesocyclones with core diameters (CD) of 2.5, 5 and 10 km. The abscissa is the average mean rotational velocity that is indicated by the curves down the center of the shaded bands in Fig. 26.

The curves in Figs. 24 and 27 all show that the coverage area for detecting mesocyclone and tornadic vortex signatures doubles with 0.5o AZ, compared to 1.0o AZ. The coverage area increases because mesocyclones and tornadoes have stronger Doppler velocity signatures with 0.5o AZ at all ranges from the radar. Therefore, it is advisable for all new convective storm VCPs to use azimuthal increments of 0.5o instead of 1.0o.

The times in Table 1 do not allow for 0.5o azimuthal sampling. In order to have acceptable reflectivity and Doppler velocity uncertainties, the fast antenna rotation speeds may have to be slowed down a little. One should note, however, that the elevation angles in Table 1 are independent of antenna rotation speed.

6. A look at an initial elevation angle of 0.3o

Smith (1998) investigated the question of how low a radar beam can scan without suffering loss of reflectivity and Doppler velocity information owing to part of the beam intercepting the ground. He concluded that the antenna can be lowered to 0.3 beamwidth above the radar horizon before detrimental effects start to appear. For the WSR-88D, with a beamwidth of about 0.95o, the lowest reasonable elevation angle is 0.3o.

A set of VCPs starting with 0.3o is listed in Table 2. Compared with the VCPs in Table 1, most of those in Table 2 go to higher elevation angles and take longer to complete the full volume scan. For some of the VCPs, the increased time is due to an additional elevation angle below 1.45o, where two complete scans are made at each elevation angle.

For shallow phenomena, the lowest elevation angle dictates how close to the ground and how far away from the radar that the phenomenon can be detected and therefore warned upon. Computations show that, by decreasing the lowest elevation angle to 0.3o, the maximum detection range would increase by about 15 km at closer ranges and by about 20 km at ranges from 115 to 230 km. Also, the detection height would be lower by 0.2 km at 60 km, 0.4 km at 115 km and 0.8 km at 230 km. Though these improvements appear to be minimal, they can produce an incremental increase in the detectability of shallow phenomena that extend to heights of only 1-3 km. If the public can be convinced that lowering the elevation angle does not pose a health hazard, then it would be advisable to decrease the lowest elevation angle to 0.3o.

7. Recommendations

Among other things, the WSR-88D is used to estimate precipitation and to detect the presence of damaging storms. Two volume coverage patterns (VCPs), VCP 11 and VCP 21, currently are available to handle these situations. However, users have found that the VCPs do not always provide the information they need. So, for several years, they have been requesting that changes (such as those listed in the Introduction) be made. We undertook this study to develop some new VCPs that help to satisfy the users' needs. We assume that each WSR-88D operates independently and that the region immediately surrounding the radar does not benefit from coverage by other radars.

The new VCPs that we developed exhibit two basic characteristics that are new: they are flexible and they are optimized. By "flexible", we mean that the VCP stops after the radar clears the tops of all radar return . By "optimized", we mean that the maximum percentage of height uncertainty is essentially the same no matter the height or range of a particular feature. A brief discussion of these and other characteristics that should be included with new VCPs is presented below. It should be kept in mind, however, that these recommended changes cannot be implemented until software changes are made to most of the WSR-88D algorithms.

1. Optimized VCPs (Section 3). We developed a technique for computing "optimized" VCPs. The maximum height underestimate (expressed as a percentage) owing to finite increments between elevation angles is essentially the same at all heights and all ranges. Besides providing a logical increase in the separation of elevation angles with increasing elevation angle, the technique assures adequate sampling of distant storms. We recommend that all future VCPs be developed using this optimization technique.

2. Flexible VCPs (Section 4). To improve temporal resolution without sacrificing vertical resolution, the VCPs used by the WSR-88D should be flexible. That is, there should be an algorithm that ends a volume scan after detecting two consecutive elevation angles having no radar return. We recommend that all future VCPs be flexible, so that, when conditions merit, a VCP can be ended before it reaches the maximum elevation angle.

3. Faster VCPs (Section 4). The evolution of some severe weather phenomena (such as tornadoes and downbursts) is so rapid that forecasters are at a disadvantage in issuing warnings based on 5- and 6-minute VCPs. Faster VCPs will improve the warning process. By the time that fast VCPs are implemented, the communication links will have been upgraded so they can handle the increased flow of information. In addition to using flexible VCPs for decreasing volume scan time, we recommend that all future VCPs use maximum antenna rotation rates that are consistent with specified maximum Doppler velocity and reflectivity estimates of error.

4. Improve horizontal resolution (Section 5). Simulations of WSR-88D data collected in model mesocyclones and tornadoes show that the range of mesocyclone and tornadic vortex signature detection increases by 50% when data are collected at 0.5o instead of the conventional 1.0o azimuthal increment. This increase is equivalent to doubling the detection area. We recommend that all VCPs developed for convective storm detection collect data using a 0.5o azimuthal increment.

5. Increase the maximum elevation angle (Sections 3 and 4). The current VCPs 11 and 21 do not tilt higher than 19.5o. The volume of space between 19.5 and 90o is literally a "cone of silence", where the radar cannot detect storm features. The narrow band of data that appears on a PPI display at high elevation angles is difficult for a human to interpret. Also, Doppler velocity measurements at higher elevation angles contain a significant bias from precipitation fall speeds. However, the higher elevation angles provide a wealth of additional reflectivity information to the algorithms that ultimately benefits the users. Therefore, we recommend that all optimized VCPs include elevation angles up to 60o, which is the mechanical upper limit for the antenna.

6. Decrease the lowest elevation angle (Section 6). A theoretical study suggests that the WSR-88D antenna can be lowered to 0.3o without degrading WSR-88D reflectivity and Doppler velocity measurements. Decreasing the lowest elevation angle from 0.5o to 0.3o will increase the range of detection by 15-20 km. Also, at a given range, it will lower the height of the lowest data points by 0.4 km at 115 km range and by 0.8 km at 230 km range. Though these improvements appear to be minimal, they can be significant in dealing with convective phenomena that are only 1-3 km deep. We recommend that the lowest elevation angle be decreased to 0.3o.

7. Make algorithm developers/modifiers aware of upcoming VCP changes. At the present time, new VCPs cannot be added to the WSR-88D system until changes are made to some of the algorithms. Users have been requesting VCP changes for years, but nothing has happened because there is no easy way to modify the algorithms. We are proposing changes that likely will affect all of the WSR-88D algorithms. In preparation for these changes, we recommend that algorithm developers and modifiers be mandated to add flexibility to their algorithms that will easily allow changes to be made to such parameters as elevation angle (from negative angles for mountaintop radars up through 60o), number of elevation angles, horizontal azimuthal increment, rotation rate, VCP recycle time, etc.

8. Replace VCP 11 and VCP 21. VCPs 11 and 21 do not do a very good job in resolving nearby and far-range convective storms. Using the optimization technique developed for this study, we prepared new VCPs A and B that include the types of changes that forecasters have requested to help them with issuing more timely and accurate warnings. We recommend that VCP 11 and VCP 21 be replaced with optimized VCPs, such as those typified by VCP A and VCP B (fast rotation rates, elevation angles from 0.3o to 60o for non-mountaintop radars, horizontal azimuthal increment of 0.5o, ability to end the VCP partway through the sequence).

References

Brown, R. A., and V. T. Wood, 1998: Technique for improving WSR-88D detection of tornadoes. Preprints, 19th Conf. on Severe Local Storms, Minneapolis, Amer. Meteor. Soc., 721-724.

Brown, R. A., L. R. Lemon and D. W. Burgess, 1978: Tornado detection by pulsed Doppler radar. Mon. Wea. Rev., 106, 29-38.

Greene, D. R., and R. A. Clark, 1972: Vertically integrated liquid: A new analysis tool. Mon. Wea. Rev., 100, 548-552.

Greene, D. R., J. D. Nilsen, R. E. Saffle, D. W. Holmes, M. D. Hudlow and P. R. Ahnert, 1983: RADAP II, An interim radar data processor. Preprints, 21st Conf. on Radar Meteor., Edmonton, Amer. Meteor. Soc., 404-408.

Howard, K. W, J. J. Gorley, and R. A. Maddox, 1997: Uncertainties in WSR-88D measurements and their impacts on monitoring life cycles. Wea. Forecasting, 12, 166-174.

Kingsmill, D. E., and R. M. Wakimoto, 1991: Kinematic, dynamic, and thermodynamic analysis of a weakly sheared severe thunderstorm over northern Alabama. Mon. Wea. Rev., 119, 262-297.

Maddox, R. A., D. S. Zaras, P. L. MacKeen, J. J. Gorley, R. Rabin and K. W. Howard, 1999: Echo height measurements with the WSR-88D: Use of data from single versus two radars. Wea. Forecasting, 14 (in press).

Mahoney, E. A., and R. Schaar, 1993: WSR-88D scan strategy impacts on the vertically integrated liquid product. Preprints, 26th Intern. Conf. on Radar Meteor., Norman, OK, Amer. Meteor. Soc., 44-46.

Roberts, R. D., and J. W. Wilson, 1989: A proposed microburst nowcasting procedure using single-Doppler radar. J. Appl. Meteor., 28, 285-303.

Saffle, R. E., 1976: D/RADEX products and field operation. Preprints, 17th Conf. on Radar Meteor., Seattle, Amer. Meteor. Soc., 555-559.

Smith, P. L., 1998: On the minimum useful elevation angle for weather surveillance radar scans. J. Atmos. Ocean. Technol., 15, 841-843.

Torgerson, K. L., and R. A. Brown, 1996: Radar signatures of updrafts within the Carson, ND hailstorm of 11 July 1989. Preprints, 18th Conf. on Severe Local Storms, San Francisco, Amer. Meteor. Soc., 81-85.

Wood, V. T., and R. A. Brown, 1997: Effects of radar sampling on single-Doppler velocity signatures of mesocyclones and tornadoes. Wea. Forecasting, 12, 928-938.

Wood, V. T., and R. A. Brown, 1998: Improved detection capability of single-Doppler velocity signatures of far-range mesocyclones. Preprints, 19th Conf. on Severe Local Storms, Minneapolis, Amer. Meteor. Soc., 717-720.