2. Procedure
Table1. Comparison of elevation angles (deg) for VCP 11, VCP 22 (modified VCP 11) and VCP 21.
VCP 11 VCP 22 VCP 21 0.5 0.5 0.5 1.45 1.45 1.45 2.4 2.4 2.4 3.35 3.35 3.35 4.3 4.3 4.3 5.25 - 6.2 6.2 6.0 7.5 - 8.7 - 10.0 10.0 9.9 12.0 - 14.0 14.0 14.6 16.7 - 19.5 19.5 19.5
Melbourne, FL KMLB 25-26 March 1992 1947-0755 UTC Frederick, OK KFDR 8 May 1993 1044-2319 UTC.
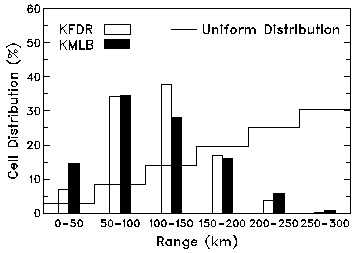
Figure 1. Distribution of radar-detectable cells at 50-km intervals for the KFDR and KMLB data sets. The stepped line is the distribution that would arise if cells were uniformly distributed within 300 km range of a radar.
WSR-88D Storm Cell Identification and Tracking (SCIT) Algorithm -- maximum reflectivity, height of maximum reflectivity, height of 30-dBZ reflectivity contour
WSR-88D Vertically Integrated Liquid (VIL) Algorithm (cell-based) -- VIL
WSR-88D Hail Detection Algorithm (HDA) -- probability of hail, probability of severe hail, maximum expected hail size
WSR-88D Mesocyclone Algorithm (MESO) -- mesocyclone depth, maximum rotational velocity, maximum azimuthal shear, integrated rotational strength index
NSSL Mesocyclone Detection Algorithm (MDA) -- mesocyclone depth, maximum rotational velocity, maximum azimuthal shear, mesocyclone strength rank, mesocyclone strength index
NSSL Tornado Detection Algorithm (TDA) -- signature depth, maximum gate-to-gate velocity difference, maximum gate-to-gate shear
NSSL Neural Network (NN) Probabilities -- probability of tornado, probability of severe winds
3. Storm Cell Identification and Tracking (SCIT) Algorithm
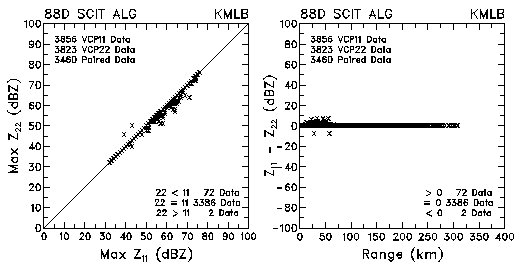
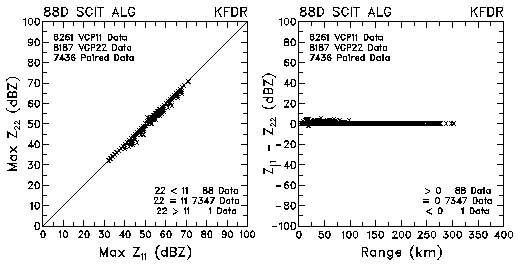
Figure 2. Plots of maximum reflectivity values and reflectivity differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR.
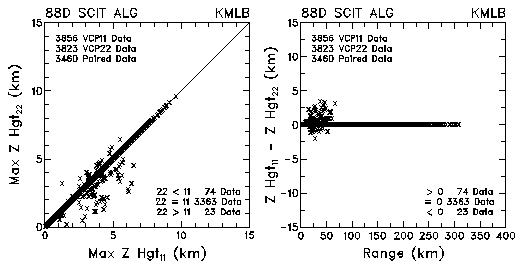
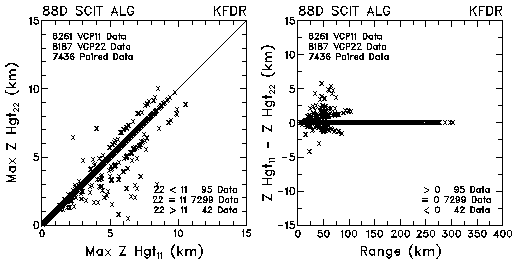
Figure 3. Plots of heights of maximum reflectivities and height differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The cause of the radial bands is discussed in the text.
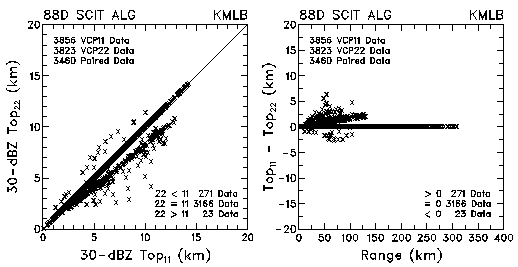
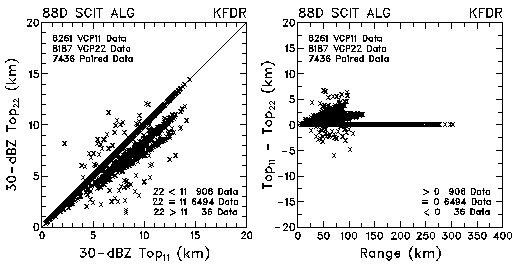
Figure 4. Plots of the heights of 30-dBZ tops of storm cells and height differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The cause of the radial bands is discussed in the text.
4. Vertically Integrated Liquid (VIL) Algorithm
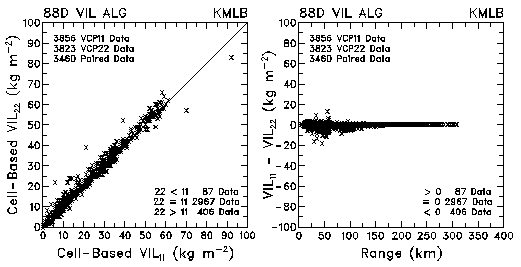
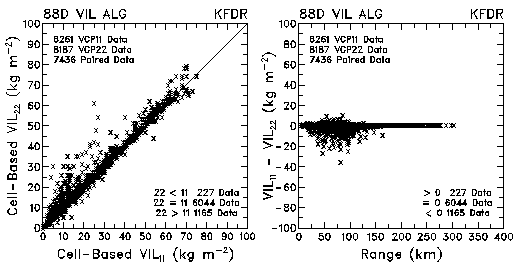
Figure 5. Plots of VIL and VIL differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR.
5. WSR-88D Hail Detection Algorithm (HDA)
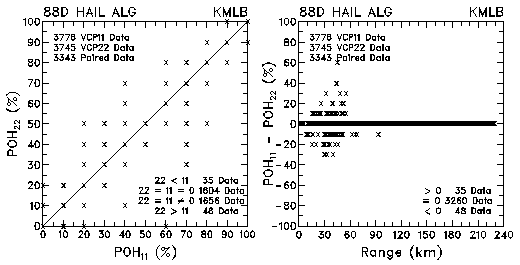
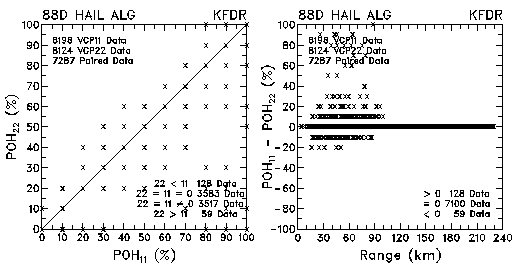
Figure 6. Plots of probability of hail (POH) and probability differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR.

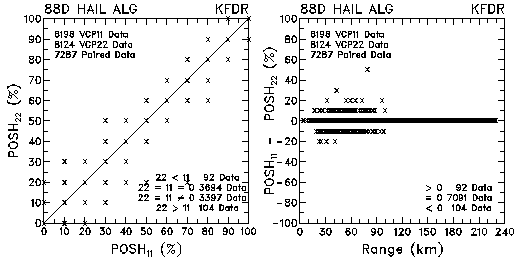
Figure 7. Plots of probability of severe hail (POSH) and probability differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR.
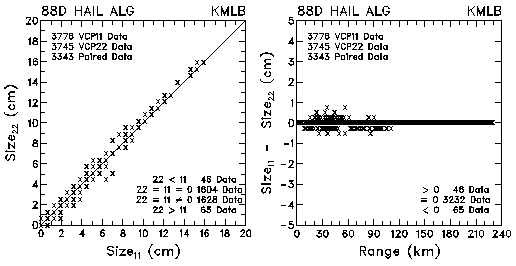
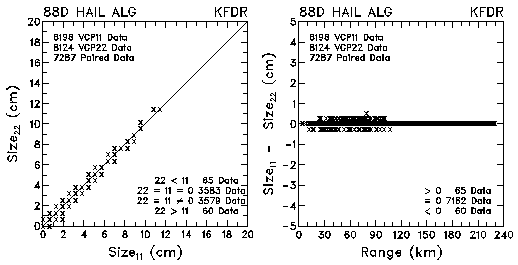
Figure 8. Plots of maximum expected hail size and size differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR.
6. WSR-88D Mesocyclone Algorithm (MESO)
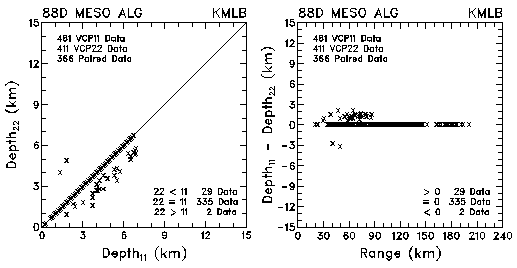
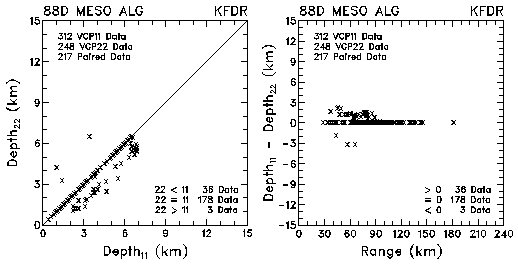
Figure 9.Plots of mesocyclone depth and depth differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the WSR-88D Mesocyclone Algorithm.
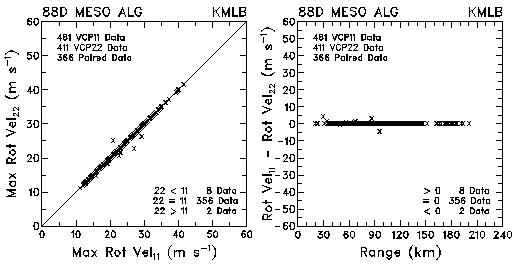
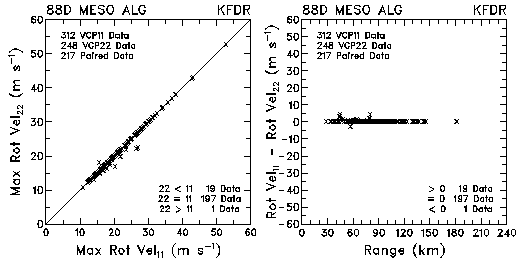
Figure 10. Plots of maximum rotational velocity and velocity differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the WSR-88D Mesocyclone Algorithm.
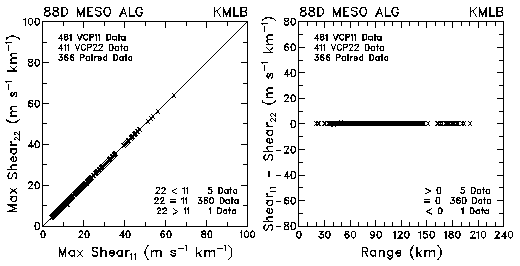
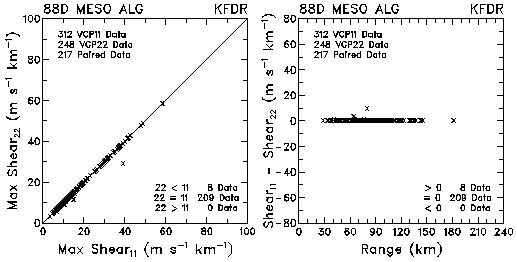
Figure 11. Plots of maximum shear and shear differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the WSR-88D Mesocyclone Algorithm.
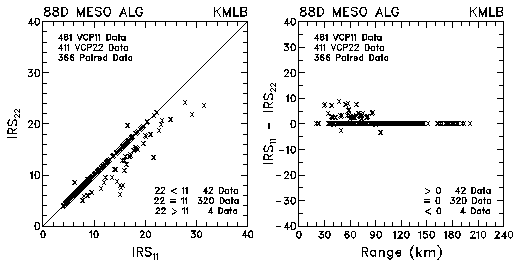

Figure 12. Plots of integrated rotational strength (IRS) index and IRS index differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the WSR-88D Mesocyclone Algorithm.
7. NSSL Mesocyclone Detection Algorithm (MDA)
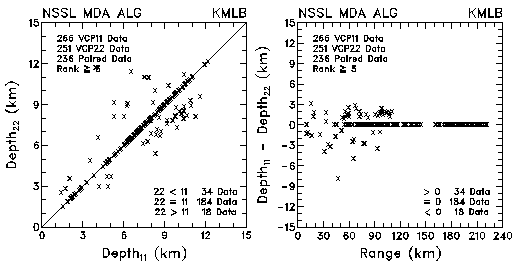
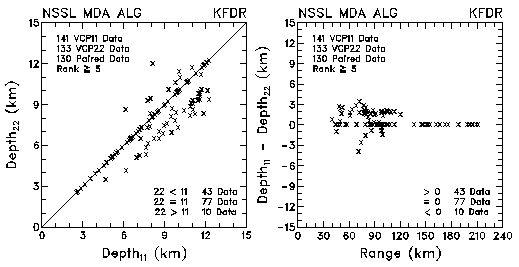
Figure 13. Plots of mesocyclone depth and depth differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Mesocyclone Detection Algorithm.
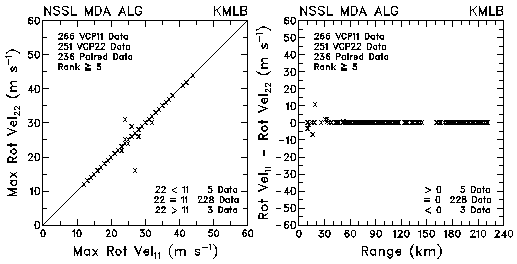
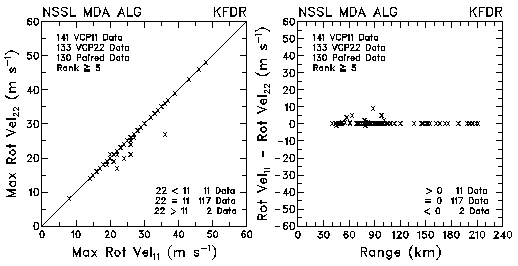
Figure 14. Plots of maximum rotational velocity and velocity differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Mesocyclone Detection Algorithm.
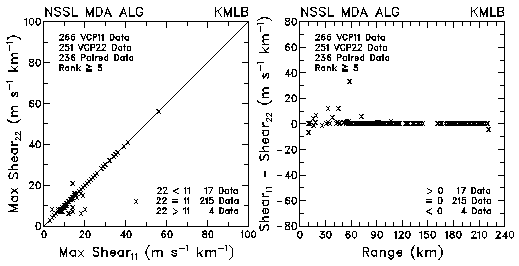
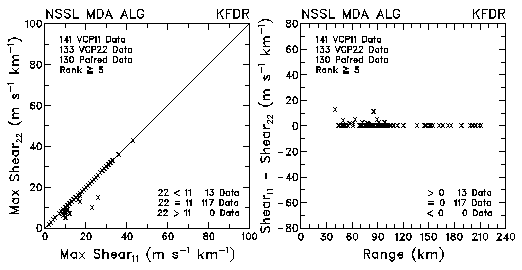
Figure 15. Plots of maximum shear and differences in shear values between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Mesocyclone Detection Algorithm.
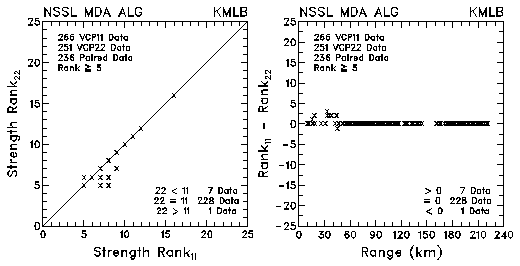
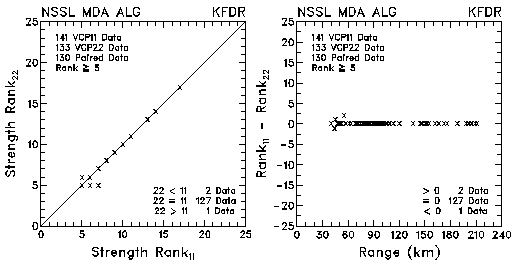
Figure 16. Plots of 3D strength rank and differences in strength rank between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Mesocyclone Detection Algorithm.
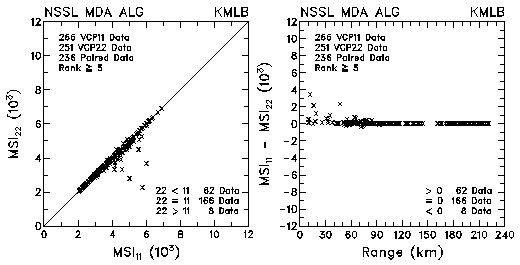

Figure 17. Plots of mesocyclone strength index (MSI) and differences in index values between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Mesocyclone Detection Algorithm.
8. NSSL Tornado Detection Algorithm (TDA)

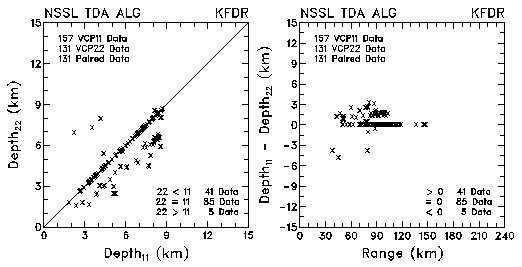
Figure 18. Plots of (E)TVS depth and differences in depth values between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Tornado Detection Algorithm.
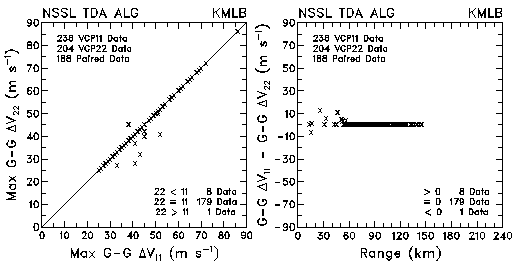
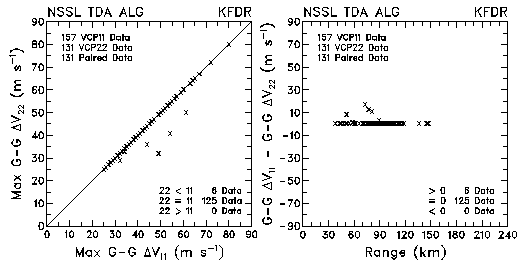
Figure 19. Plots of maximum gate-to-gate azimuthal Doppler velocity differences and differences in the velocity difference values between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Tornado Detection Algorithm.
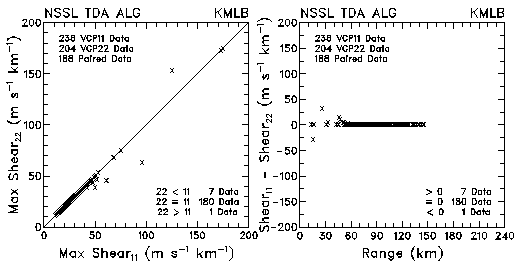
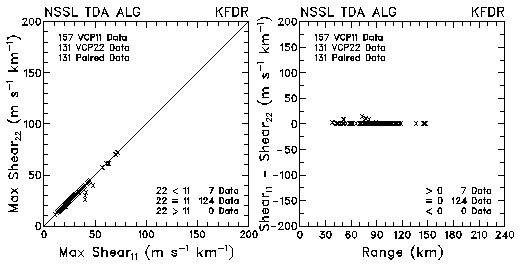
Figure 20. Plots of maximum azimuthal shear and differences in the shear values between VCP 11 and VCP 22 for data collected by KMLB and KFDR. The plots are based on the NSSL Tornado Detection Algorithm.
9. NSSL Neural Network (NN) Probabilities
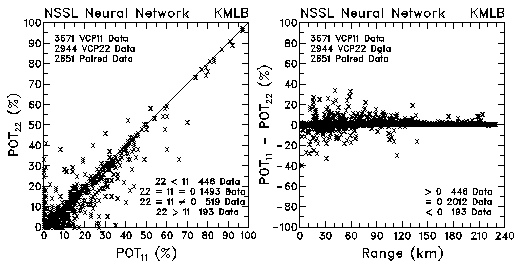
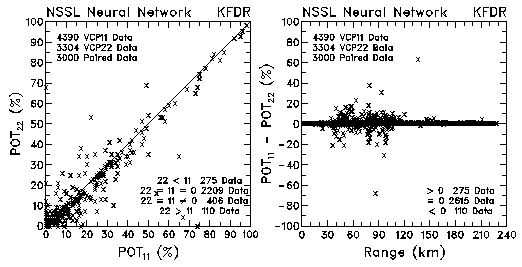
Figure 21. Plots of probability of tornado occurrence (POT) and probability differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR.
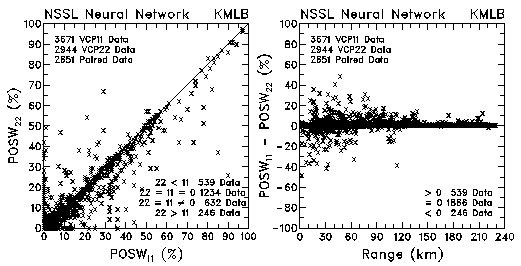
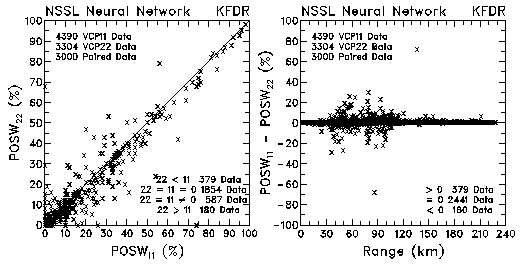
Figure 22. Plots of probability of severe winds (POSW) and probability differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR.
10. Velocity Azimuth Display (VAD) Algorithm
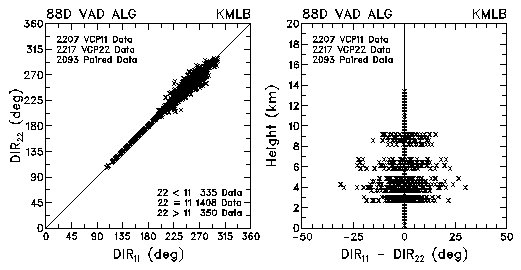
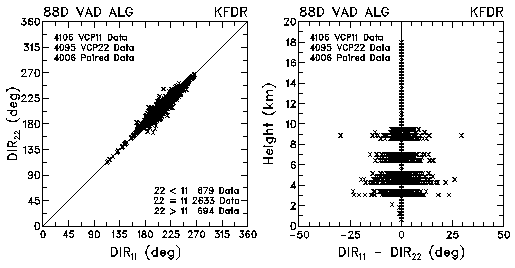
Figure 23. Plots of VAD wind direction and direction differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. Heights are relative to sea level.
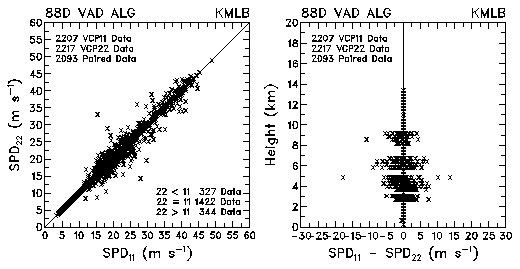
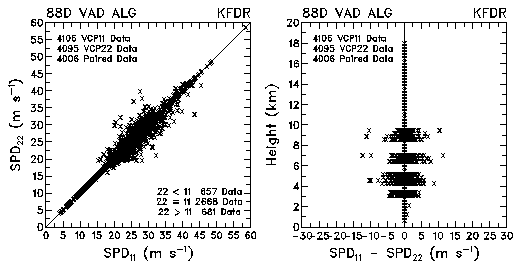
Figure 24. Plots of VAD wind speed and speed differences between VCP 11 and VCP 22 for data collected by KMLB and KFDR. Heights are relative to sea level.
11. Concluding Comments
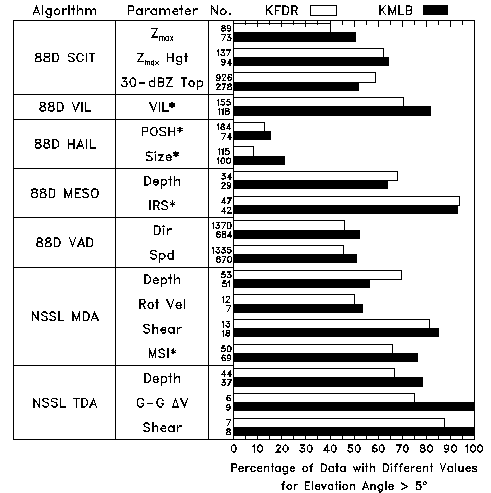
Figure. 25. Percentage of algorithm parameter values that were different using VCP 11 and VCP 21/22 when the elevation angle of the parameter was greater than 5o; missing elevation angles above 5o for VCP 21/22 produce the different values. The numbers in the third column are the number of paired data points that were different for each radar. Asterisks indicate those parameters that arise from vertical integration; the 5o threshold applies to the top of the integration column.
Brown, R. A., L. R. Lemon and D. W. Burgess, 1978: Tornado detection by pulsed Doppler radar. Mon. Wea. Rev., 106, 29-38.
Fulton, R. A., J. P. Breidenbach, D.-J. Seo, D. A. Miller and T. O'Bannon, 1998: The WSR-88D rainfall algorithm. Wea. Forecasting, 13, 377-395.
Greene, D. R., and R. A. Clark, 1972: Vertically integrated liquid: A new analysis tool. Mon. Wea. Rev., 100, 548-552.
Johnson, J. T., P. L. MacKeen, A. Witt, E. D. Mitchell, G. J. Stumpf, M. D. Eilts and K. W. Thomas, 1998: The storm cell identification and tracking algorithm: An enhanced WSR-88D algorithm. Wea. Forecasting, 13, 263-276.
Lee, R. R., and A. White, 1998: Improvement of the WSR-88D mesocyclone algorithm. Wea. Forecasting, 13, 341-351.
Lhermitte, R. M., and D. Atlas, 1961: Precipitation motion by pulse Doppler radar. Proc. Ninth Wea. Radar Conf., Amer. Meteor. Soc., 218-223.
Marzban, C., and G. J. Stumpf, 1996: A neural network for tornado prediction based on Doppler radar-derived attributes. J. Appl. Meteor., 35, 617-626.
_____, and _____, 1998: A neural network for damaging wind prediction. Wea. Forecasting, 13, 151-163.
Mitchell, E. D., S. V. Vasiloff, G. J. Stumpf, A. Witt, M. D. Eilts, J. T. Johnson and K. W. Thomas, 1998: The National Severe Storms Laboratory tornado detection algorithm. Wea. Forecasting, 13, 352-366.
Stumpf, G. J., A. Witt, E. D. Mitchell, P. L. Spencer, J. T. Johnson, M. D. Eilts, K. W. Thomas and D. W. Burgess, 1998: The National Severe Storms Laboratory mesocyclone detection algorithm for the WSR-88D. Wea. Forecasting, 13, 304-326.
Witt, A., M. D. Eilts, G. J. Stumpf, J. T. Johnson, E. D. Mitchell and K. W. Thomas, 1998: An enhanced hail detection algorithm for the WSR-88D. Wea. Forecasting, 13, 286-303.