
(Revised 1 October 1998)
Comments to Harold Brooks
The following are some, perhaps, disjointed items related to the frequency of tornado occurrence and death rate in the United States. They are intended to convey some of the challenges associated with looking at the observed record, particularly for the purpose of conveying anything to do with changing climate. It has been proposed that extreme weather events will increase in frequency in an enhanced greenhouse-gas climate. Tornadoes seem a natural event to consider in that light. The nature of the record, however, makes it difficult to do. That does not mean that there will not be a change in tornadoes in a greenhouse-gas climate, but that it may not be possible to see that change, particularly without giving some thought to the statistics to be examined. In particular, we want to look for stable parameters, which perhaps give us some hope of detecting changes. For this beginning effort, I'm going to look at only national numbers. No regionalization has been done and none will be done in the near future.
A second purpose of this effort is to try to put 1998's large death toll into a historical perspective.
I'd like to acknowledge Tom Grazulis for providing much of the data used here, Chuck Doswell for constructive comments, and Dan Wilks for a suggestion on treatment of the Markov chain that made the problem tractable.
A good starting point is the observed record of all tornado reports. The figure below shows the number of tornado reports since 1954 (including an estimate for 1998, based on how many had been reported through the end of June and extrapolating to the end of the year, based on the percentage of reports typically observed in the first half of the year.)

The red line gives the raw number of reports, the black line is a linear least squares fit to the data from 1954-1997, and the blue line is an adjusted value, of which I'll say more in a minute. There is clearly a long-term increase in the number of tornado reports since the 1950s, with the average number now twice the value we reported in the '50s. The least squares line has a slope of 12 reports/year. The adjusted values were created by assuming that the ratio of the reports to the value of the regression line for a particular year was "correct" and that the "true" mean number of reports was the value reported in 1997. In effect, I'm assuming that big years compared to the long-term trend were, in fact, big years (and not just anomalies in the reporting process). Things that stand out from that approach are that 1957 (Dallas, Ruskin Heights, Fargo, etc) and 1973 were really big years and that 1998 is the only year to threaten their records since then. In addition, the early 1970s were a big period for tornadoes and the late 1980s were really, really poor. Perhaps, the timing of the beginning of "scientific" storm chasing was fortuitous.
The reasonably good record of tornado deaths goes back further in time, but convolves tornadoes and demographic changes. The raw tornado death record in the US (below) illustrates how deadly the 1920s in particular were.

The black line represents a simple filter applied to the data (3-point median, followed by a 5-point running mean on the median). The filtered data shows that the deadliness of the 1920s doesn't just rest with 1925. 1920, 1924, 1929, and especially 1927 were all big death toll years. In the last 50 years, the only big spikes in the raw record are 1965 and 1974, both of which rest on single large outbreaks for the majority of their deaths. From this picture, one might get the idea that we have the tornado death problem licked. However, ....
An instructive approach to looking at the tornado death record is to normalize the number of deaths by the US population. That provides a different picture, as seen below.

The data have been plotted on a log-scale for clarity. The thin, pink line shows the raw data. The thick, red line is a filtered (3-pt median, followed by 5-pt running mean) version of the data. The green lines are least squares fits to the filtered data from 1880-1924 and then 1925-1997 (the equations are given by the "Fit = " statements). In the earlier period, the death rate was almost constant at 1.8 deaths/million people. Since 1925, we've seen a steady decline in the death rate, to the point that the value at 1997 is 0.14 deaths/million. I cannot explain the decrease. Lots of things contribute--improved forecasts and warnings, communication of warnings, better housing, the movement of people from rural areas to urban areas, less time being spent outdoors, etc. (Before we, in the meteorological and preparedness communities pat ourselves on the back, it is important to note that lightning deaths also show a decreasing trend over this time period, but we do little forecasting or preparedness work on that problem, in comparison to tornadoes.) As an aside, there are no statistically significant differences between El Niño, La Niña, and other years.
The cyan lines represent the 10th and 90th percentiles over the period from 1925 to the present, with respect to the regression line over that time period. By this measure, 1998 is the third deadliest year of the century (124 deaths through the middle of July). Only 1953 and 1974 are worse. 1998 is comparable to (and slightly ahead of) 1925 and 1965. For comparison, there were 794 fatalities in 1925 or 7 deaths/million population. A similar rate in 1998 would have resulted in 1823 deaths. A possible interpretation of that is that roughly 1700 lives have been saved, in 1998 alone, by whatever mechanisms have led to the decreasing death rate.
There are obviously large societal and scientific issues raised by this result and I certainly am not confident enough to take it too far. It is, however, one of the more interesting figures I've seen.
As a possible candidate for a stable variable representing something about tornadoes, I decided to look at the number of significant tornado (F2 or greater) days per year in the United States. Simply put, if a tornado rated at F2 or greater occurs on a day, that's a significant tornado day. If 100 significant tornadoes occur on a single day, that counts as one day, also. To look at this with a longer record than the Storm Prediction Center has, I've used Tom Grazulis's book, Signficant Tornadoes 1680-1991 and the update through 1995. The number of significant tornado days per year has been relatively stable since 1921, as seen below.

The black dots are the raw data and, again, the line is a filtered version of it. It's possible that the 1970s were a big time, or that the 1990s have represented a decrease, but, given the scatter of the data, I'm not too confident about that. The most days we've seen since 1921 in any year was 80 in 1954. The least has been 33 in 1987. Over the 75 year period, the mean number of days has been about 53/year, with a standard deviation of 9. As an aside, there are no statistically significant differences between El Niño, La Niña, and other years.
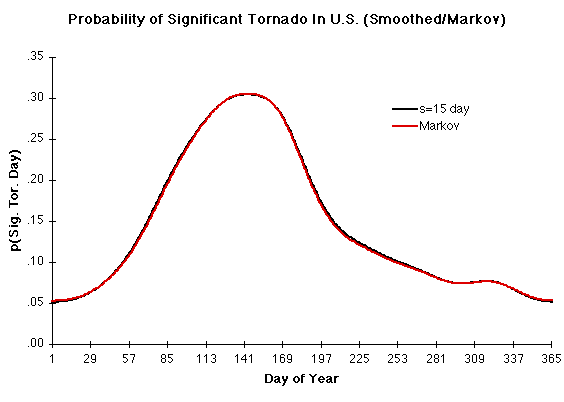
The annual cycle is equally interesting. I've plotted the data as the probability of a significant tornado day occurring by day of year.

The peak raw value (red dots) is 0.48 (7 June). A more realistic estimate of the probability can be obtained by smoothing the raw data. In this case, I've used a more powerful smoother--applying a Gaussian to the values. The degree of smoothing is determined by the parameter s, which is the standard deviation, in days, of the Gaussian. Here, I show two smoothers-3 and 15 days. There is a double peak apparent in the 3-day smoother in late May and early June, followed by a sharp dropoff in the probability of a significant tornado day. The stronger smoother changes that double peak into a single peak (p~0.3), centered on 22-23 May. In either case, the increase in probability at the beginning of "tornado season" is somewhat slower than the decrease at the end of the season. The first day of the year with a value of pł0.25 for the s=15 day case is 12 April, 40 days before the peak, while the last day is 25 June, 33 days after the peak.
Even in the strongly smoothed case, a second relative peak in significant tornado day frequency occurs in late October to late November when the seasonal decrease in tornado occurrence reverses, giving a peak probability (s=15 day) of .077 (14 Nov). The minimum probability is ~0.05 at the end of December and beginning of January.
As part of looking at the significant tornado days, I looked at runs of consecutive days with and without significant tornadoes. Over the 75-year period from 1921-1995, the longest run of days with significant tornadoes is 9 (15-23 May 1949 and 6-14 June 1967). The longest run without a significant tornado is 115 days (17 September 1962-9 January 1963). I tried to reproduce the variability of runs and of number of significant tornado days per year by just using the probability of significant tornado day occurrence as a function of the day of the year, but the model didn't capture the extremes at all.
As a result, I developed a first-order Markov chain model. In a nutshell, a Markov chain model calculates the probability of an event occurring based on the previous state of the system using transition probabilities, or how likely the state is to change to some other state at the next step. A first-order model only cares about what the last state of the model was. In the specific case of tornado days, if a significant tornado occurs on day n of the chain, the probability of a a significant tornado occurring on day n + 1 is just a function of the occurrence on day n, and is different than the probability of a tornado occurring if a significant tornado did not occur on day n. For the tornado problem, there are 4 transition probabilities: p00 (probability of no tornado on day n+1, given that no tornado occurred on day n), p01 (probability of tornado on day n+1, given that no tornado occurred on day n), p10 (probability of no tornado on day n+1, given that a tornado occurred on day n), and p11 (probability of tornado on day n+1, given that a tornado occurred on day n).
After looking at the observed runs when significant tornadoes are most and least likely, I decided to model the transition probabilities as linear functions of the smoothed (s=15 days) probability of a significant tornado. I only had to model two of the transition probabilities, since the other two could be obtained by using the fact that the sum of the probabilities of mutually exclusive, completely exhaustive events is 1. The linear functions for p11 and p01 are shown below, as well as the resultant probabilities as a function of time of year.


Armed with the transition probabilities, I could run the Markov chain and get statistical estimates of the likelihood of long runs or number of significant tornado days during the year. A run of 75 years shows the kind of variability seen in the observations, but somewhat longer runs (10 million years, in this case) provide nice statistical data sets. First, for a reality check, the chain reproduces the annual cycle of tornado days, as seen below.
Perhaps more importantly, the chain gives estimates of the likelihood of seeing certain numbers of tornado days in a given year. The probability distribution function of tornado days is nearly Gaussian, as seen below.

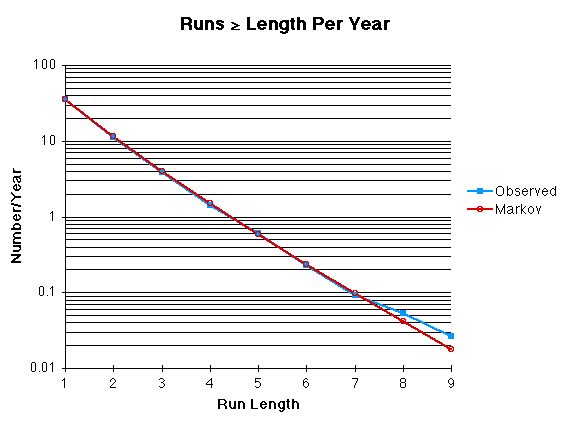
There is a 10% chance of having 43 or fewer days in a given year and a 10% chance of more than 63 days, as indicated by the cyan lines. In the observational record, there are 10 days (out of 75, or 13%) in each of those ranges. The Markov model may be slightly conservative, but not much. Over the course of the 10,000,000 year run, runs as long as 25 consecutive days with tornadoes occurred, as well as runs with 215 days without significant tornadoes.
Comparison with the observed probability of long runs shows that the model does quite well in estimating the observed record:
Finally, due to the changes in the unconditional probability of a significant tornado day over the course of the year, unconditonal values of p11 (and the other transition probabilities) ends up having a dependence on the length of the run, even though the transition probabilities, conditioned by time of year, are not functions of the run length. (Since p11 varies by more than a factor of 2 over the course of the year, long runs during winter don't occur. Thus, all of the data from long runs come from April-June. As a result, the unconditional probability of a tornado given 4 consecutive days with tornadoes is higher than the unconditional probability of a tornado given 2 consecutive days with tornadoes. I've compared the two modelled and observed transition probabilities, p11 and p00, by length of the run without regard for time of year. The results are shown below. Clearly the Markov chain model does a good job of estimating this derived statistical occurrence.


I hope to exploit the Markov chain in the future. It makes it possible to estimate the likelihood of rare events. If, for instance, we start seeing several runs of 12 consecutive days with significant tornadoes, the extreme unlikelihood of that event makes it probable that either the reporting base of significant tornadoes or the meteorological conditions in which they form has changed. It is also possible to estimate the likelihood of changes in the timing of the spring and fall maxima of significant tornado days. Those estimates may allow us to determine if anything at all can be said about detection of climate change using tornado data.
As well as the national probability of a significant tornado day, I've computed the probability for each state, based on the 1921-1995 data. With a similar smoothing as before, here is a graph of the annual cycle for a number of states.
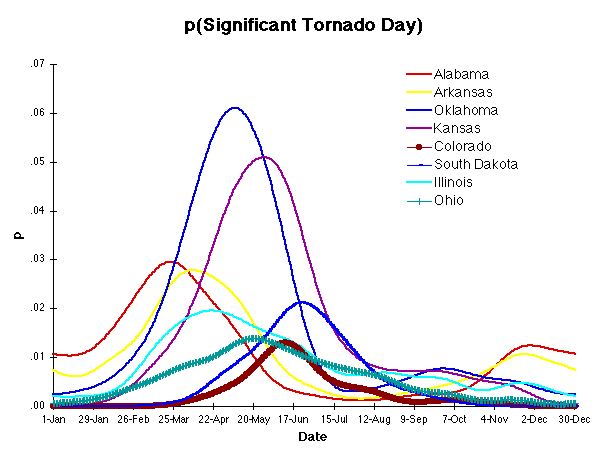
The annual march of maximum tornado frequency shows up nicely: starting in mid-March in the southeast, as illustrated by Alabama, moving west through Arkansas and Oklahoma, where a sharp increase in peak probability is seen, and then marching north with decreasing peak probability through the Dakotas. The Plains season is concentrated in a relatively short period of time and is symmetric, in contrast to the states from Missouri eastward (illustrated by Illinois and Ohio), where the distribution is much flatter and skewed towards later in the year.
Note that Oklahoma shows a small secondary peak around the first of October (Kansas has a slight hint, in that the curve stops decreasing, while Arkansas and Alabama show distinct peaks in November/December at almost half of their primary peak.
Normalizing the probability by area doesn't change the picture very much, but before anyone asks, here it is:
