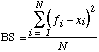 . (1)
. (1)
Driscoll (1988) discussed the relationship of televised weather forecasts to those available from the National Weather Service (NWS) from a small number of sites around the US for forecasts of lead time up to 36 hours. He found that the accuracy of temperature forecasts and probability of precipitation (PoP) forecasts was not greatly different for the telecasters and the NWS. Thornes (1996) showed results of a study of the accuracy of public forecasts in the UK, but it was based primarily on one verification parameter, the "percent correct". As Murphy (1991) pointed out, the large dimensionality of the verification problem means that single measures of forecast quality can be misleading. Brooks and Doswell (1996) illustrated this idea with an example of the information available from what Murphy and Winkler (1987) described as a distributions-oriented approach to forecast verification.
To help fill (ever so slightly) this vast data void, we set out to record and verify public weather forecasts for the Oklahoma City area for a 14 month time period. Our purposes here are to illustrate some aspects of the differences in the forecast sources for a single location. In passing, we will show the utility of using information from more than one source to produce a forecast with more information (Brown and Murphy 1996). The analysis is by no means comprehensive, but it is illustrative of the power of diagnostic forecast verification techniques to provide insight into the forecast process both for the user and the forecaster.
We computed seasonal accuracy statistics as well. For the NWS, the MAE for maximum temperature forecasts was highest during the winter (Table 2). The seasonal difference is large enough that a Day 5 forecast during the summer has a lower MAE than a Day 1 forecast during the winter. Note also the difference in performance between the two winters. The forecasts, particularly at Days 2-4, were much better in the second winter. The reasons for this difference are beyond the scope of this paper. The media forecasts (not shown) show similar behavior, highlighting the difficulty of cool season temperature forecasting, at least in Oklahoma City. The minimum temperature forecasts have less extreme seasonality for all forecast sources (not shown).
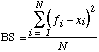 . (1)
. (1)
The Brier Skill Score (SS) is the percentage improvement, relative to a climatological baseline,
![]() , (2)
, (2)
where BSC is the Brier score with a constant climatological forecast and BSF is the Brier score of the forecast system being compared to it. Positive (negative) values of the skill score indicate the percentage improvement (worsening) of the forecast source compared to climatology.
The SS of both FS#1 and FS#2 get worse with increasing lead time (Fig. 1). This is to be expected as, typically, the forecasts get harder with time. By Day 3 for FS#1 and Day 4 for FS#2, the skill scores for the forecasts become 5% or less better than climatology. In other words, the forecasts would be almost as accurate if climatology was used in place of the actual forecast at those lead times4. By Day 7, the forecasts are 15% and 7% worse than climatology for FS#1 and FS#2, respectively.
The primary reason for the poorer skill scores at long lead time is the increasingly dry bias of the forecasts as lead time increases. The mean PoP of the forecasts decreases with lead time (Fig. 2). One would expect the long-range PoP to approach the climatological frequency. Instead, with the exception of FS#2's Day 7 forecast, the forecast PoPs approach zero. Indeed, the use of 0% as a forecast value generally increases with lead time and so does the frequency of occurrence of precipitation with a zero PoP, until it almost reaches the value of the sample climatological frequency of precipitation (Table 3).
The Day 4 maximum temperature forecasts demonstrate another useful application of the distributions-oriented approach to verification. To illustrate another way of reducing the dimensionality of the verification problem, we have defined the forecast as being a forecast of the departure from climatology and then binned the forecasts and observations into 5 šF bins, centered on values divisible by five. All departures greater than or equal to 25 šF are put into the ± 25 šF bin. Comparisons of FS #2 and FS #4 are particularly interesting (Table 5.) Note that the Day 4 maximum represents the only one of the ten temperature forecasts (maximum and mininum) for which FS #2 does not have the lowest MAE and, in fact, FS #2 has the highest MAE for this forecast variable (see Table 1). In this case, FS #4 has the lowestMAE. However, if we consider the number of forecasts in correct 5 šF bins, FS #2 has the largest number of correct forecasts of any source (95 or 28%) in the correct bin, and FS #4 has the fewest (84 or 25%). The apparent inconsistency between these two results occurs because FS #2 has the most forecasts more than two categories away from the observations (54 or 16%), and FS #4 has the fewest (41 or 12%). Thus, although FS #2 is more likely to be nearly correct, it is also more likely to be in serious error. Any ranking by accuracy depends upon the definition of accuracy used. As a result, it is not surprising that competing forecast sources can all claim to be the most accurate without "fudging" the data! As pointed out by Murphy (1993), the issue of which forecast has the most value to a user depends upon that user's needs and sensitivities. It is likely that different users may find the forecasts from different sources to be most valuable.
The variety of forecasts available to consumers in the area can, potentially, lead to confusion. In effect, not considering the Day 6 and Day 7 forecasts that are available from some of the television stations, there are 25 forecasts of a given day's maximum and minimum temperature. One way of combining all these forecasts is to consider the accuracy of the mean of the 25 forecasts as the level of agreement between the forecasts changes. To do so, we have calculated the variance of the 25 forecasts for each day (that is, the 5 forecasts from each of the four media sources and the NWS) and compared it to the error of the mean of all 25 forecasts. The variance of the forecasts is correlated to the absolute error of the mean forecast at a 99% confidence level for both the minimum (correlation coefficient = 0.24) and the maximum (0.44) temperature. Thus, when the forecasts agree with each other, they are much more likely to be nearly correct than when they disagree with each other. In order to look at this further, we've divided the forecasts into those cases in which the variance of the forecasts is less than or greater than 10šF2. The MAE increases with variance (Table 6). It is interesting to note that the variance in the high-temperature forecasts is quite a bit larger than in the low-temperature forecasts. 182 forecasts met the low-variance criterion for the minimum temperature forecast, while only 149 did so for the maximum temperature forecast. Other things being equal, one might expect more variance in the maximum temperature forecasts, since they have a slightly longer lead time and, more importantly, since the variance of maximum temperatures is greater than that of minimum temperatures (the standard deviation of observed minimum temperatures in this data set is 7.9 šF and that of the observed maximum temperatures is 9.3 šF) . Given the other results, it seems the maximum temperatures were harder to forecast during this 14 month period.
All of the television forecasters have the opportunity to use the NWS forecast as input into their forecasts6, so we have considered the quality of the forecasts when the private sector forecasts disagree strongly with the NWS. To do this, we have stratified the forecasts by counting the number of times the private forecast disagreed with the NWS forecast and was closer to the observations when the forecasts disagreed by 5 šF or more (Table 7). Only FS#2 increases the number of disagreements monotonically with increasing lead time of the forecast, if both maximum and minimum temperature forecasts are combined (i.e., Day 1 minimum, Day 1 maximum, Day 2 minimum, Day 2 maximum, etc.). FS#2 also improves on the NWS forecast significantly (at the 99% confidence level) for three out of the ten forecast periods7. There is a slight tendency, in general, for the media forecasts to be more accurate for disagreements at long lead times (Days 4-5) compared to short lead times (Days 1-2). This is particularly obvious for FS#1's maximum temperature forecast, where the source's forecasts are significantly worse than the NWS for Days 1 and 2 and significantly better at Day 5 (Table 7b). For the most part, however, the question of whether the private forecasts are more accurate than the NWS, by this measure, represents little more than a coin flip. We offer no speculations about whether specific forecast strategies lead to the patterns or lack thereof. At the moment, they are a curiosity, although it seems obvious that an understanding of the kinds of situations in which they improve (or do not improve) on the NWS forecast would be critical to any of the private sector forecasters, if they are interested in improving the quality of their forecasts.
A more general aspect of this problem that forecast users have to deal with on a regular basis is what to do with conflicting forecasts from the media sources8. We have broken the forecasts out into those cases when any one of the forecast sources goes "out on a limb" and disagrees with all the others by 5 šF or more and compared it to the mean of the other forecasts (Table 8). As might be expected, in general, a forecast that disagrees by that much from any other is likely to be wrong. FS#3 is the only source that does not do significantly worse statistically than the mean of the other forecasts when it disagrees with the others. It also finds itself in that situation less often than any of the other private forecasts, perhaps indicating that the forecasters preparing FS#3's forecasts are more conservative than the other private forecasters. Table 8b also reinforces the earlier discussion about the interesting Day 4 maximum temperature forecast for FS#2. FS#2 takes more risks on that element than any other forecast source on any element and, in the process, does worse than the mean forecast at a 99% confidence level.
Overall, we see an increase in error of the mean forecast with increasing variance of the forecasts and significant differences in the performance of the various forecast sources when they disagree strongly with the NWS. These facts indicate the need for weather-information sensitive users in the public to attempt to collect information from a variety of sources to get the most complete picture of the likely evolution of the weather. The relationship between variance and forecast error suggests that it is possible to quantify the uncertainty in the forecasts and, perhaps, to derive a probabilistic temperature forecast from the information. Clearly, no one source is sufficient to provide all of the useful information available within the media market.
FS#2 typically produced a "wetter" forecast, although it was still dry compared to climatology. About 23% of FS#2's forecasts are PoPs exceeding the climatological frequency of precipitation, whereas only 12% of FS#1's forecasts are "wet." This difference extends up to the highest probabilities, with FS#2 using PoPs exceeding 60% 22 times (8 after Day 1), including a Day 3 100% PoP. In contrast, FS#1 used PoPs exceeding 60% only 13 times (never after Day 1).
1) FS#1 had the least biased temperature forecasts, but had the highest MAE for maximum temperature forecasts.
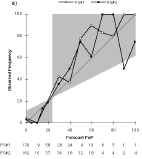
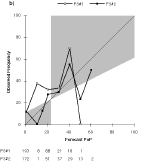
2) FS#2 had the lowest MAE for nine of the ten temperature lead times, but has the largest MAE for the Day 4 maximum forecasts. It was also the most likely to be correct when it disagreed with NWS forecasts for minimum temperatures. For the longest lead time forecasts, the observed frequency of precipitation on forecasts of 0% PoPs is higher than the observed frequency for 20% PoPs.
3) FS#3 was the most likely to be correct when it disagreed with NWS forecasts for maximum temperatures and was the most likely to be correct when it disagreed with all of the other sources overall for temperature forecasts. It was the most conservative forecast source, disagreeing with the NWS temperature forecast much less often than any of the other sources.
4) FS#4 was the least accurate minimum temperature forecast at every lead time, but was the most accurate for the Day 4 maximum.
Examination of the forecasts from sources available to the public provides fertile ground for verification specialists. More importantly, it should allow the forecasters to evaluate their own strengths and weaknesses and help in improving their products, if the quality of these forecasts is a primary concern. From what we have seen, many of the weaknesses could be improved very easily. One area of obvious improvement would be to have the long-term PoP forecasts tend towards climatology, rather than zero. Another easy improvement would be to produce unbiased temperature forecasts for the various lead times. Given that we have been able to see this, it seems that the sources under examination 1) have not verified their own forecasts, or 2) their perception of what the public wants is different than providing the highest-quality forecast, or 3) they believe that the value of their forecasts is high even if the quality is not. Given the wide range of needs of the users of publicly available forecasts and the complex relationship between quality and value, it seems unlikely that the last goal could be accomplished in any easy way. Neither of the other two options is satisfying from the public perspective. It is possible that media forecasters perceive the higher ratings as a more important goal than forecast accuracy. While this is plausible from their perspective, it may lead to forecasting strategies that do not lead to accurate forecasts. If so, we view this as a lamentable outcome and one that does not serve the public interest well. We encourage them to make forecast quality a higher priority in their process.
Further, our results highlight poor uses of probability in precipitation forecasts, as discussed by Vislocky and Fritsch (1995). The extreme dry bias at long range is indicative of a lack of understanding (or failure to apply understanding) of climatological information. This is even without discussing the use of colloquialisms to describe the chance of precipitation in the absence of numerical probabilities or the use of verbal descriptions that are inconsistent with the numbers presented in the forecast (e.g., "Our next chance of precipitation is towards the end of the week, but for now, I'll go with just an increase in cloudiness. So, you'll need to keep watching to see how things develop.") This approach can only lead to confusion in the minds of the forecast users, the public. We find it particularly distressing given the results of Murphy et al. (1980) and Sink (1995) indicating that the public understands and prefers numerical, rather than verbal, probability of precipitation forecasts.
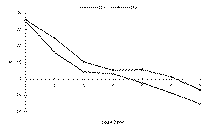
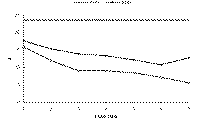
Fig. 2: Mean forecast PoP by lead time for FS#1 and FS#2. Horizontal heavy line indicates long-term climatological frequency of precipitation.
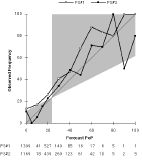
a) Day 1 (FS#2 used 5% 1 time and 15% 15 times.)
b) Day 4 (FS#2 used 15% 16 times.)
c) Day 7 (FS#2 used 15% 16 times.) Total number of forecasts is 321 for each plot.
a) MINIMUM TEMPERATURE
| FS# 1 | FS# 1 | FS# 2 | FS# 2 | FS# 3 | FS# 3 | FS# 4 | FS# 4 | NW S | NW S | ME AN | ME AN | |
| DA | MA E | Bias | MA E | Bias | MA E | Bias | MA E | Bias | MA E | Bias | MA E | Bias |
| 1 | 2.9 | .2 | 2.7 | .3 | 2.8 | .4 | 3.2 | 1.0 | 2.9 | .6 | 2.7 | .5 |
| 2 | 3.9 | .1 | 3.4 | .3 | 3.7 | .5 | 4.0 | 1.4 | 3.6 | .9 | 3.4 | .6 |
| 3 | 4.9 | .0 | 4.2 | -.1 | 4.6 | .2 | 5.0 | 1.5 | 4.8 | .1 | 4.2 | .3 |
| 4 | 5.4 | .0 | 4.9 | -.1 | 5.1 | .2 | 5.7 | 1.4 | 5.5 | .0 | 4.9 | .3 |
| 5 | 5.5 | -.1 | 5.3 | .0 | 5.6 | .2 | 6.1 | 1.4 | 5.8 | .1 | 5.3 | .3 |
| T | 4.5 | .0 | 4.1 | .1 | 4.3 | .3 | 4.8 | 1.4 | 4.5 | .3 | 4.1 | .4 |
| FS# 1 | FS# 1 | FS# 2 | FS# 2 | FS# 3 | FS# 3 | FS# 4 | FS# 4 | NW S | NW S | ME AN | ME AN | |
| DA | MA E | Bias | MA E | Bias | MA E | Bias | MA E | Bias | MA E | Bias | MA E | Bias |
| 1 | 3.9 | .3 | 3.6 | .2 | 3.8 | .6 | 4.2 | .7 | 3.8 | .6 | 3.7 | .5 |
| 2 | 5.2 | .1 | 4.8 | .1 | 4.8 | .8 | 5.1 | .9 | 4.8 | .8 | 4.7 | .6 |
| 3 | 6.2 | -.3 | 5.8 | -.1 | 5.9 | .5 | 5.9 | .7 | 5.9 | .3 | 5.6 | .2 |
| 4 | 6.7 | -.3 | 6.7 | .0 | 6.6 | .4 | 6.4 | .6 | 6.7 | .4 | 6.3 | .2 |
| 5 | 7.2 | -.3 | 7.1 | .3 | 7.2 | .7 | 7.3 | 1.0 | 7.5 | .7 | 6.9 | .5 |
| T | 5.8 | -.1 | 5.6 | .1 | 5.7 | .6 | 5.8 | .8 | 5.8 | .6 | 5.4 | .4 |
| DA | Winter1 | Spring | Summer | Autumn | Winter2 |
| 1 | 5.2 | 3.9 | 2.4 | 3.4 | 4.4 |
| 2 | 6.9 | 5.6 | 2.9 | 4.2 | 5.0 |
| 3 | 8.7 | 6.7 | 3.2 | 5.5 | 5.9 |
| 4 | 10.2 | 7.2 | 3.3 | 6.0 | 6.6 |
| 5 | 10.4 | 7.9 | 4.0 | 6.5 | 8.0 |
| T | 8.3 | 6.2 | 3.1 | 5.1 | 6.0 |
| DA | FS#1 | FS#1 | FS#2 | FS#2 |
| 0% Usage | Obs. Freq. | 0% Usage | Obs. Freq. | |
| 1 | 53.0 | 4.1 | 50.5 | 3.1 |
| 2 | 56.7 | 8.8 | 52.6 | 5.9 |
| 3 | 64.5 | 12.1 | 54.8 | 11.4 |
| 4 | 60.1 | 11.4 | 53.6 | 11.6 |
| 5 | 62.9 | 14.4 | 52.6 | 11.2 |
| 6 | 66.0 | 17.9 | 56.4 | 13.3 |
| 7 | 72.6 | 20.2 | 43.6 | 20.0 |
| Obs. | ||||||||
| 20 | 25 | 30 | 35 | 40 | 45 | p(f) | ||
| 20 | 14 | 2 | 0 | 0 | 0 | 0 | .045 | |
| 25 | 5 | 7 | 3 | 0 | 0 | 0 | .042 | |
| Fcst. | 30 | 2 | 8 | 13 | 3 | 1 | 0 | .076 |
| 35 | 0 | 3 | 11 | 10 | 7 | 0 | .087 | |
| 40 | 0 | 0 | 3 | 6 | 16 | 7 | .090 | |
| 45 | 0 | 0 | 0 | 0 | 8 | 227 | .660 | |
| p(x) | .059 | .056 | .084 | .053 | .090 | .657 | 1.000 |
| FS# 2 | Obs . | ||||||||||||
| -25 | -20 | -15 | -10 | -5 | 0 | 5 | 10 | 15 | 20 | 25 | N (f) | ||
| -25 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| -20 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 5 | |
| -15 | 2 | 1 | 6 | 1 | 2 | 6 | 0 | 0 | 0 | 0 | 0 | 18 | |
| -10 | 2 | 1 | 5 | 8 | 6 | 3 | 6 | 3 | 0 | 0 | 0 | 34 | |
| -5 | 1 | 1 | 4 | 13 | 17 | 8 | 10 | 4 | 2 | 1 | 0 | 61 | |
| For e. | 0 | 1 | 1 | 4 | 9 | 17 | 24 | 17 | 8 | 0 | 0 | 0 | 81 |
| 5 | 1 | 0 | 0 | 5 | 6 | 17 | 21 | 15 | 7 | 2 | 2 | 76 | |
| 10 | 1 | 0 | 0 | 1 | 4 | 1 | 7 | 14 | 2 | 5 | 0 | 35 | |
| 15 | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 7 | 2 | 3 | 2 | 20 | |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 1 | 0 | 5 | |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| N (x) | 9 | 6 | 21 | 38 | 53 | 62 | 65 | 52 | 16 | 12 | 4 | 28 |
b)
| FS# 4 | Obs . | ||||||||||||
| -25 | -20 | -15 | -10 | -5 | 0 | 5 | 10 | 15 | 20 | 25 | N (f) | ||
| -25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| -20 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| -15 | 2 | 3 | 3 | 3 | 1 | 1 | 0 | 2 | 0 | 0 | 0 | 15 | |
| -10 | 1 | 0 | 7 | 8 | 6 | 5 | 4 | 1 | 0 | 0 | 0 | 32 | |
| -5 | 2 | 1 | 7 | 8 | 13 | 9 | 10 | 3 | 1 | 0 | 0 | 54 | |
| For e. | 0 | 2 | 1 | 3 | 13 | 22 | 25 | 14 | 8 | 2 | 1 | 0 | 91 |
| 5 | 0 | 0 | 0 | 5 | 8 | 16 | 17 | 19 | 5 | 3 | 2 | 75 | |
| 10 | 0 | 0 | 0 | 1 | 3 | 5 | 17 | 15 | 6 | 2 | 0 | 49 | |
| 15 | 1 | 0 | 0 | 0 | 0 | 1 | 3 | 4 | 1 | 5 | 2 | 17 | |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| N (x) | 9 | 6 | 21 | 38 | 53 | 62 | 65 | 52 | 16 | 12 | 4 | 25 |
| Min T | Min T | Max T | Max T | |
| Var. | MAE | Var. | MAE | |
| Overall | 11.9 | 3.7 | 16.1 | 5.0 |
| Low Var. | 5.3 | 2.9 | 5.4 | 3.4 |
| High Var. | 19.5 | 4.6 | 24.6 | 6.4 |
Table 6: Variance and MAE of mean temperature forecasts for cases with variance of forecasts <10šF2 (Low Var.) and >10šF2 (High Var.).
a) MINIMUM TEMPERATURES
| DA | 1 | 2 | 3 | 4 | 5 | Total |
| FS#1 |
| 33 (41) | 46 (76) | 60 (77) | 57 (96) | 52 (304) |
| FS#2 | 69 (13) | 45 (20) | 68 (63) | 71 (80) | 55 (95) | 63 (271) |
| FS#3 | 50 (16) | 43 (21) | 58 (54) | 61 (51) | 56 (73) | 56 (217) |
| FS#4 | 52 (27) | 41 (38) | 50 (100) | 46 (107) | 46 (133) | 47 (405) |
| DA | 1 | 2 | 3 | 4 | 5 | Total |
| FS#1 | 29 (21) | 30 (47) | 49 (65) | 51 (80) | 60 (127) | 50 (340) |
| FS#2 | 56 (27) | 52 (42) | 50 (83) | 49 (100) | 62 (112) | 54 (364) |
| FS#3 |
| 39 (29) | 58 (54) | 64 (61) | 60 (72) | 56 (236) |
| FS#4 | 35 (44) | 46 (54) | 48 (103) | 55 (112) | 55 (130) | 50 (443) |
a) MINIMUM TEMPERATURES
| DA | 1 | 2 | 3 | 4 | 5 | Total |
| FS#1 | 0 (3) | 22 (10) | 24 (18) | 39 (13) | 31 (13) | 27 (57) |
| FS#2 | -- (0) | 50 (2) | 60 (5) | 64 (14) | 42 (12) | 55 (33) |
| FS#3 | 50 (4) | 25 (4) | 43 (7) | 40 (5) | 46 (13) | 42 (33) |
| FS#4 | 40 (5) | 44 (9) | 11 (18) | 8 (13) | 30 (20) | 23 (65) |
| NWS | 0 (1) | -- (0) | 25 (4) | 22 (9) | 27 (11) | 24 (25) |
| DA | 1 | 2 | 3 | 4 | 5 | Total |
| FS#1 | 0 (4) | 21 (15) | 43 (7) | 33 (13) | 32 (22) | 29 (61) |
| FS#2 | 50 (6) | 50 (4) | 29 (17) | 21 (25) | 53 (15) | 35 (66) |
| FS#3 | 0 (3) | 50 (2) | 50 (8) | 46 (11) | 56 (18) | 48 (42) |
| FS#4 | 25 (12) | 44 (9) | 24 (21) | 35 (23) | 35 (17) | 32 (82) |
| NWS | 100 (1) | 0 (2) | 10 (10) | 38 (8) | 22 (23) | 23 (44) |