3. INTERPRETATION OF DOPPLER VELOCITY PATTERNS WITHIN TROPICAL CYCLONES
Until the advent of weather satellites, conventional weather radars on the coasts and occasional reconnaissance aircraft penetrations provided the primary means for tracking the movement of tropical cyclones as they approached land. When satellites became available, the tracking capability was extended back to the point of origin and thus it became possible to monitor the evolution of tropical cyclones for many days as they moved toward land. Conventional radars and satellites provide general clues about storm strength and reconnaissance aircraft provide periodic estimates of maximum wind speeds. However, it was not until WSR–88D Doppler radars became operational in the early 1990s that one could continuously measure the maximum speeds within a storm as it approached the coastline.
In this chapter, we discuss how the storm-relative Doppler velocity pattern in a tropical cyclone changes as distance from the radar decreases. In order to present the basic features, we make a number of simplifying assumptions. We assume that the Doppler velocity pattern is due only to flow rotating around the cyclone center—axisymmetric and approximated by a Rankine combined vortex. A Rankine combined vortex consists of two regions: within the core region, tangential velocity increases linearly from zero at the center to the maximum speed at the edge of the core region; beyond the core region, tangential velocity changes (decreases) inversely proportional to distance from the circulation center. In order to depict changes in circulation appearance that are due only to changes in range, we further assume that the circulation structure is constant with height. Lastly, we assume that radar reflectivity is uniform across the tropical cyclone; with the absence of spiral rainbands, one is able to view the entire circulation without any of it missing owing to the lack of reflectivity.
Shown in Figs. 3.1–3.3 are simulated tropical cyclones at decreasing distances from a coastal Doppler radar. The maximum rotational velocity of 60 m s-1 (117 kt) occurs at a radius of 25 km (13.5 n mi) from the circulation center. Because the Nyquist velocity is only ±30 m s-1, the peak Doppler velocity values of both +60 and -60 m s-1 are aliased to 0 m s-1 (for example, 60 m s-1 – 2 x 30 m s-1 = 0 m s-1). Since a Doppler radar measures only the component of motion toward or away from the radar, the Doppler velocity signature of an axisymmetric circulation includes zero Doppler velocity in the radial direction from the radar through the circulation center where flow is perpendicular to the radar viewing direction. As discussed in section 2.2, wind speed on the ground at the radar location is equal to the highest Doppler velocity contour that passes through the radar location. With the simulated cyclone 160 km from the radar (Fig. 3.1), the estimated surface wind speed at the radar site is 5–10 m s-1 (10–19 kt); at 80 km range (Fig. 3.2), it is 15–20 m s-1 (29–39 kt); and at 30 km range (Fig. 3.3), it is about 50 m s-1 (97 kt).
Peak Doppler velocity values occur at the edge of the core region where the radial viewing direction is tangent to the circle of maximum wind. As a tropical cyclone moves toward the radar, the points where radial lines are tangent to the circle (location of maximum wind) move closer together on the side of the core region nearer the radar (e.g., Wood and Brown 1992). This trait becomes apparent at 80 km range (Fig. 3.2) and is very obvious at 30 km range (Fig. 3.3). Even though the Doppler velocity pattern becomes increasingly distorted as the cyclone moves toward the radar, the peak Doppler velocity value is unaffected until the core region is over the radar.
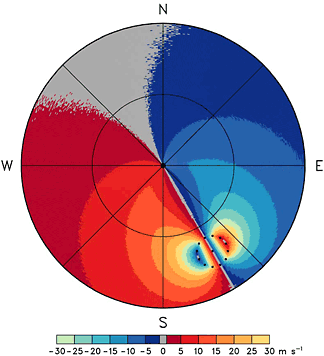
Fig. 3.1. Simulation of storm-relative Doppler velocities in a tropical cyclone at a range of 160 km (86 n mi) from a coastal Doppler radar (center of display). The two range circles are at distances of 115 (62) and 230 km (124 n mi) from the radar. The dotted circle surrounding the cyclone center (small dot) indicates the edge of the core region where the maximum winds are found. (larger image)
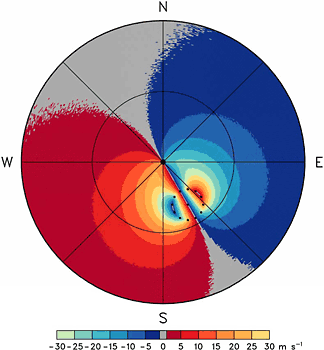
Fig. 3.2. Same as Fig. 3.1, except the tropical cyclone center is at a range of 80 km (43 n mi) from the radar. The overall Doppler velocity pattern is similar to that simulated by Baynton (1979). (larger image)
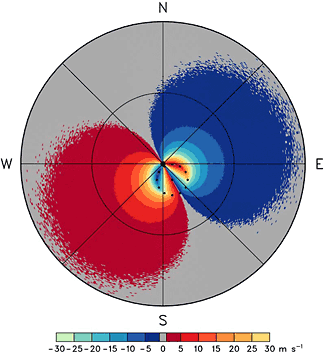
Fig. 3.3. Same as Fig. 3.1, except the tropical cyclone center is at a range of 30 km (16 n mi) from the radar. Note that the area of each Doppler velocity interval has been decreasing outside the core diameter (dotted circle), except for the near zero interval that has been increasing, as the tropical cyclone approaches the radar (Figs. 3.1 through 3.3). If an axisymmetric tropical cyclone were centered on the radar, all Doppler velocity values would be zero because the entire flow field would be perpendicular to all radial viewing directions. (larger image)
NSSL HOME >> DOPPLER GUIDE HOME >> CONTENTS >> CHAPTER 3 >> CHAPTER 4