1. BACKGROUND INFORMATION
1.1 Introduction
Doppler radars have been used to study weather phenomena throughout the world since the mid 1950s (e.g., Rogers 1990). Initially, Doppler radars were used by the weather research and engineering communities to study phenomena ranging from clear air to severe thunderstorms. As the advantages of Doppler radars over conventional weather radar became known, interest developed in using Doppler radars for real-time operational applications. By the mid-1990s, Weather Surveillance Radar–1988 Dopplers (WSR–88Ds) and Terminal Doppler Weather Radars (TDWRs) were in operational use in the United States. WSR–88Ds are used for overall weather surveillance and warnings by the National Weather Service, U. S. Air Force, and Federal Aviation Administration (FAA). TDWRs are used by the FAA at selected airports to monitor wind conditions that would adversely affect aircraft take-offs and landings.
A Doppler radar typically measures three base data parameters: radar reflectivity factor (function of scatterer intensity), mean Doppler velocity within the radar sampling volume (function of the mean component of scatterer motion in the radial direction from the radar) and spectrum width (function of the variability of Doppler velocity values due to turbulence within and velocity shear across the sampling volume). Interpretations of reflectivity and Doppler velocity data acquired from quasi-horizontal radar scans are based primarily on the identification of recognizable reflectivity and Doppler velocity patterns or "signatures."
Computer algorithms are routinely used with WSR–88Ds for automatically processing the data and identifying significant Doppler velocity and reflectivity features. These derived products are available to the radar user shortly after the data are collected. Algorithms developed for WSR–88Ds are discussed in Federal Meteorological Handbook 11, Part C (OFC 2006) as well as in other publications, such as the papers that appeared in the June 1998 issue of Weather and Forecasting. Even with the availability of algorithm output, forecast and warning decisions frequently require user interpretation of Doppler velocity signatures on radar displays.
The goal of this Guide is to acquaint prospective users with the interpretation of Doppler velocity signatures. Through the use of simulated Doppler velocity displays, the reader is introduced to a number of patterns associated with basic subsynoptic-scale, mesoscale, and storm-scale flow patterns.
1.2 Review of Doppler Radar Principles
a. Concept of Range Folding
A pulse Doppler radar, like a conventional weather radar, transmits a series of pulses that are separated by a distance, d, in the radial direction from the radar (e.g., Battan 1973; Rinehart 2004). The separation distance is a function of the rate at which pulses are transmitted (PRF, pulse repetition frequency) and the speed, c, at which radar energy propagates through the atmosphere
d = c/PRF ,
where c is 3 x 108 m s-1 (5.8 x 108 kt). Some of the transmitted energy is reradiated back to the radar by scattering regions (precipitation, insects, refractivity gradients, etc.). The maximum range to which a pulse can travel and return before the next pulse is transmitted is one-half the separation distance, d. This maximum range is defined as
rmax = c/(2 PRF) .
The range of a scattering region from the radar is computed from the time that the pulse is transmitted until signal is received back at the radar. The tacit assumption is that the returned signal is from the pulse that was just transmitted. If the scattering region is at a range greater than rmax, return from that region will not be received by the radar until after the next pulse is scattering region is between rmax and 2 rmax. For a constant PRF, the radar processing equipment is not able to distinguish between range r and ranges r + rmax (second trip), r + 2 rmax (third trip), or r + 3 rmax (fourth trip). Measurements from all trips are "folded" back into the first trip interval. Thus, all measured ranges are potentially ambiguous because, without additional information, it is not possible to determine the proper trip to which a returned signal should be assigned. Design of the WSR–88D and its scanning strategies permit range-folded Doppler velocity and spectrum width data to be recovered and placed into the proper range interval or trip (e.g., Doviak and Zrnić 1993, pp. 175–177). This may not be true for other Doppler radars.
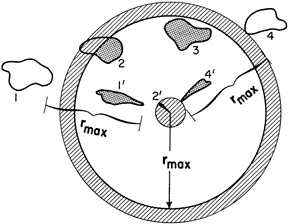
Fig. 1.2.1. Examples of range folding for a line of four storms oriented from the WSW to the ENE. The circle at distance rmax from the radar is the end of the first trip. Shaded areas represent the locations of measured radar return (radar "echoes"); those labeled with primed numbers were received from storms located beyond the first trip. Hatched area at center represents radar return from ground targets. If the second trip were displayed, all echoes in the first trip would be repeated in the second trip (echoes corresponding to the shaded portions of storms 2 and 3 would appear as wider echoes beyond the top of the figure); the ground return around the radar would appear as the shaded ring at the beginning of the second trip. (larger image)
The process of range folding is illustrated in Fig. 1.2.1 for a radar that is not able to recognize and resolve range-folded radar return. The radar is at the center of the circle having a radius of rmax. The hatched region surrounding the radar location represents return from the ground and objects such as trees and buildings. North of the radar, four irregular storm regions (labeled 1, 2, 3, 4) are in a line oriented from the west-southwest toward the east-northeast. The shaded regions represent radar return measured by the radar. Storms 1 and 4 beyond the rmax circle are folded to ranges within the circle (1' and 4'). For storm 2, which straddles the circle, only the outer portion (within the second-trip ground return region) is folded back to the radar location (2'). Note that second-trip radar echoes are narrower within the first-trip domain because echo angular width is maintained and thus the linear width approaches zero with decreasing distance from the radar.
b. Concept of Doppler Velocity Aliasing
One way to alleviate the range-folding problem is to decrease the PRF until rmax is beyond all scattering regions. However, this approach introduces an additional problem for Doppler radars. The maximum Doppler velocity measuring interval (called the Nyquist cointerval) is related to the PRF and the radar wavelength, λ, by
Vmax = ± PRF λ / 4 ;
see Battan (1973) for a derivation of this expression. As the PRF decreases, Vmax decreases and a problem called Doppler velocity aliasing (analogous to range folding) occurs. Solving Eq. (1.2.3) for PRF and substituting it into Eq. (1.2.2), one finds that
Vmax rmax = ± c λ / 8
Thus, for a Doppler radar having a specific wavelength, the product of Vmax and rmax is a constant; increasing rmax decreases Vmax and vice versa. This unfortunate tradeoff between Vmax and rmax frequently is referred to as the “Doppler dilemma” (e.g., Rinehart 2004).
The process of Doppler velocity aliasing is illustrated in Fig. 1.2.2. Consider a uniform wind blowing from the west at 36 m s-1 (70 kt) at a particular height in the atmosphere. As the radar antenna rotates 360 in azimuth, the Doppler velocity at a specified range gate location (at an elevated slant range at the height of the 36 m s-1 winds) varies as a sinusoidal curve as sketched in Fig. 1.2.2. Since a Doppler radar measures the component of wind relative to the radar viewing 4 direction, a Doppler velocity value of +36 m s-1 (positive values representing flow away from the radar) occurs when the radar points toward the east (90°). When the radar points toward the west (270°), the Doppler velocity value is −36 m s-1 (negative values representing flow toward the radar). When the radar points toward the north (0°) or south (180°), the Doppler velocity value is zero because the wind is perpendicular to the radar viewing direction.
When Vmax is ±30 m s-1 (58 kt), for example, and the environmental wind is 36 m s-1, Doppler velocity values in excess of ±30 m s-1 are aliased. The portions of the solid curves in Fig. 1.2.2 represent the Doppler velocity values measured by the radar. The aliasing process causes the true Doppler velocity values to be offset by multiples of 2 Vmax until they fall within the Nyquist cointerval. Thus, +36 m s-1 is aliased to +36 − 2 x 30 = −24 m s-1 and −36 m s-1 is aliased to −36 + 2 x 30 = +24 m s-1 ; in this case, the true values are offset by only one multiple of 2 Vmax in order to fall within the ±30 m s-1 Nyquist cointerval.
Without additional information, it is not possible to determine whether an individual Doppler velocity data point has been aliased. However, spatial continuity (as in Fig. 1.2.2) permits one to readily identify visually the presence of aliasing and to make the proper adjustments. Computer algorithms are designed to objectively identify and correct aliased Doppler velocity data (e.g., Eilts and Smith 1990; Conway et al. 1995).
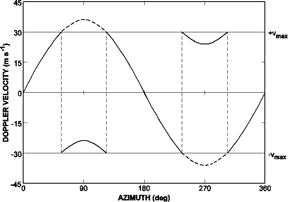
Fig. 1.2.2. Display of Doppler velocity at a given range gate as a function of azimuth when the radar antenna rotates at a fixed elevation angle. The sinusoidal curve represents true Doppler velocity measurements of a wind blowing from the west at 36 m s-1 (70 kt). The thick solid curves represent Doppler velocity values within the Nyquist cointerval of ±30 m s-1 (58 kt). (larger image)
1.3 Organization of This Guide
The Doppler velocity displays in this guide are simulated. The simulations are based on analytical functions similar to those used by Wood and Brown (1986) and Brown and Wood (1991). They also were inspired by simulated Doppler velocity patterns produced by Kraus and Donaldson (1976) and Baynton (1979), among others. The radar's beamwidth is assumed to be zero, such that there is no azimuthal smearing (degradation) of the simulated data; in reality, data degradation increases with increasing range because the linear width of the beam increases with range (angular width remains constant). Data are collected/digitized at 0.25 km (0.13 n mi) intervals in range and 1° intervals in azimuth, following the conventional sampling procedures of a WSR–88D.
In Chapter 2, simulated Doppler velocity patterns from widespread precipitation and clear air are presented on a plan position indicator (PPI) display that is a conical surface at a given elevation angle. In most cases, the wind is assumed to be horizontally homogeneous and to vary only in the vertical. But there are a few examples of more realistic wind fields where there are variations across the display. Small-scale noise and point-to-point random noise were added to the displays to give a semblance of reality.
In Chapter 3, simulated Doppler velocity patterns are presented of a tropical cyclone as it approaches a coastal radar. As the storm approaches, the Doppler velocity pattern becomes increasingly distorted.
In Chapter 4, simulated Doppler velocity patterns within convective storms are presented in blown-up windows located 100 km (54 n mi) due north of a radar; no noise was added to these data. Typical flow fields at various stages of development and altitudes within convective storms are simulated. The displays are blocky because the individual range gates are more evident than they are on the full PPI display. The horizontal wind field from which each simulated Doppler velocity display was produced also is presented.
NSSL HOME >> DOPPLER GUIDE HOME >> CONTENTS >> CHAPTER 1 >> CHAPTER 2